
| A. | ?x∈R,f(x)≤f(x0) | B. | ?x∈R,f(x)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x)≥f(x0) |
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
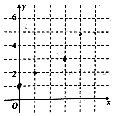 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示| x | 0 | 1 | 3 | 4 |
| y | 1 | 2 | 3 | 4.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
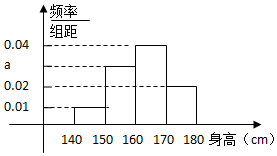 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:| 南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| 北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x3 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=3x | D. | f(x)=($\frac{1}{2}$)x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com