
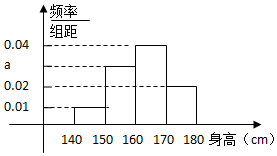
 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)分析 (1)根据0.01+0.02+a+0.04=0.1,求出a的值即可;
(2)根据中位数的左边和右边的直方图的面积相等可求中位数;计算每个小矩形的面积乘以小矩形底边中点的横坐标之和可得平均数.
(3)根据频数=频率×样本容量,可以求出身高介于140~150的学生人数和身高介于150~160的学生人数,进而由组合数公式,可求出从身高在140-160的学生中随机抽取2名学生的事件个数及至少有一个人身高在150-160之间的事件个数,代入古典概型概率公式,可得答案.
解答 解:(1)a=0.1-0.01-0.02-0.04=0.03;
(2)中位数的左边和右边的直方图的面积相等,由此可以估计中位数的值,∵0.1+0.3+0.04×2.5=0.5
所以中位数的估计值为162.5.
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
则平均数的估计值为145×0.1+155×0.3+165×0.4+175×0.2=162,
(3)这20名学生中,身高在140-150之间的有2个,分别为A,B,身高在150-160之间的有6人,
从这8人中任选2个,有${C}_{8}^{2}$=28种选法,
两个身高都在140---150之间的选法有1种选法,
所以至少有一个人在150-160之间的选法有28-1=27,
故至少有一人的身高在150-160之间的概率为$\frac{27}{28}$.
点评 本题考查了利用频率分布直方图求样本的中位数、平均数,考查了古典概型的概率计算,解题的关键是读懂频率分布直方图的数据.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)≤f(x0) | B. | ?x∈R,f(x)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x)≥f(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向左平移$\frac{π}{6}$个单位 | |
| B. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向右平移$\frac{π}{12}$个单位 | |
| C. | 先把各点的横坐标伸长到原来的2倍,再向左平移$\frac{π}{6}$个单位 | |
| D. | 先把各点的横坐标伸长到原来的2倍,再向右平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,点F在平面ABED内的正投影为G,且G在AE上,FG=$\sqrt{3}$,点M在线段CF上,且CM=$\frac{1}{4}$CF.
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,点F在平面ABED内的正投影为G,且G在AE上,FG=$\sqrt{3}$,点M在线段CF上,且CM=$\frac{1}{4}$CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com