
分析 (Ⅰ)利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,根据对称中心到最近的对称轴的距离为$\frac{π}{4}$,即$\frac{1}{4}T=\frac{π}{4}$,可得T,即求ω及f(x)的对称柚方程.
(Ⅱ)由$f(A)=\frac{{\sqrt{3}}}{4},sinC=\frac{1}{3},a=\sqrt{3}$,利用正弦定理得求b的值即可.
解答 解:函数$f(x)=cosωx•sin({ωx-\frac{π}{3}})+\sqrt{3}{cos^2}ωx-\frac{{\sqrt{3}}}{4}({ω>0,x∈R})$
化简可得:$f(x)=cosωx({\frac{1}{2}sinωx-\frac{{\sqrt{3}}}{2}cosωx})+\sqrt{3}{cos^2}ωx-\frac{{\sqrt{3}}}{4}$
=$\frac{1}{2}sinωxcosωx+\frac{{\sqrt{3}}}{2}{cos^2}ωx-\frac{{\sqrt{3}}}{4}$
=$\frac{1}{4}sin2ωx+\frac{{\sqrt{3}}}{4}({1+cos2ωx})-\frac{{\sqrt{3}}}{4}$
=$\frac{1}{4}sin2ωx+\frac{{\sqrt{3}}}{4}cos2ωx$
$\begin{array}{l}\\=\frac{1}{2}sin({2ωx+\frac{π}{3}})\end{array}$;
(Ⅰ)由函数y=f(x)图象的一个对称中心到最近的对称轴的距离为$\frac{π}{4}$,
得$\frac{1}{4}T=\frac{1}{4},\frac{2π}{2ω}=π$,解得ω=1.
当ω=1时,$f(x)=\frac{1}{2}sin({2x+\frac{π}{3}})$,
由$2x+\frac{π}{3}=\frac{π}{2}+kπ({k∈Z})$,求得$x=\frac{π}{12}+\frac{kπ}{2}({k∈Z})$.
即f(x)的对称轴方程为$x=\frac{π}{12}+\frac{kπ}{2}({k∈Z})$.
(Ⅱ)由(Ⅰ)知$f(A)=\frac{1}{2}sin({2A+\frac{π}{3}})=\frac{{\sqrt{3}}}{4}$,即$sin({2A+\frac{π}{3}})=\frac{{\sqrt{3}}}{2}$.
∴$2A+\frac{π}{3}=2kπ+\frac{π}{3}或2A+\frac{π}{3}=2kπ+\frac{2π}{3}$,
解得:A=kπ或$kπ+\frac{π}{6}$(k∈Z)
又∵A∈(0,π),
∴A=$\frac{π}{6}$.
由sinC=$\frac{1}{3}$$<\frac{1}{2}$,C∈(0,π),
∴C$<\frac{π}{6}$,
故得$cosC=\frac{{2\sqrt{2}}}{3}$.
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{\sqrt{3}+2\sqrt{2}}{6}$,
∵a=$\sqrt{3}$
由正弦定理得:b=$\frac{asinB}{sinA}=\frac{3+2\sqrt{6}}{3}$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.同时也考查了两角和与差以及正弦定理,属于中档题.


科目:高中数学 来源: 题型:解答题
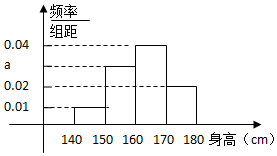 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:| 南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| 北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com