
| A�� | �ȰѸ���ĺ��������̵�ԭ����$\frac{1}{2}$����������ƽ��$\frac{��}{6}$����λ | |
| B�� | �ȰѸ���ĺ��������̵�ԭ����$\frac{1}{2}$����������ƽ��$\frac{��}{12}$����λ | |
| C�� | �ȰѸ���ĺ������쳤��ԭ����2����������ƽ��$\frac{��}{6}$����λ | |
| D�� | �ȰѸ���ĺ������쳤��ԭ����2����������ƽ��$\frac{��}{12}$����λ |
���� �����յ���ʽ��y=Asin����x+�գ���ͼ��任���ɣ��ó����ۣ�
��� �⣺�Ѻ���y=cosx=sin��x+$\frac{��}{2}$����ͼ��ĺ������Ϊԭ����$\frac{1}{2}$�����ɵ�y=sin��2x+$\frac{��}{2}$����ͼ��
�ٰ�����ͼ��������ƽ��$\frac{��}{12}$����λ���ɵ�y=sin[2��x-$\frac{��}{12}$��+$\frac{��}{2}$]=sin��2x+$\frac{��}{3}$����ͼ��
��ѡ��B��
���� ������Ҫ�����յ���ʽ��y=Asin����x+�գ���ͼ��任���ɣ����ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
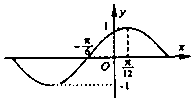
| A�� | $y=sin��{x+\frac{��}{6}}��$ | B�� | $y=cos��{2x-\frac{��}{6}}��$ | C�� | $y=sin��{2x-\frac{��}{6}}��$ | D�� | $y=cos��{4x-\frac{��}{3}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
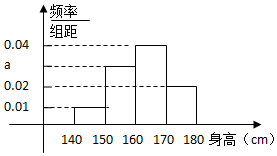 ij��ѧ�Ը����꼶��������ͳ�ƣ����������ȡ��20��ѧ�������ߣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ����λ��cm��
ij��ѧ�Ը����꼶��������ͳ�ƣ����������ȡ��20��ѧ�������ߣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ����λ��cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪б������ABC-A1B1C1�������ⳤ��Ϊ2����B1BA=$\frac{��}{3}$��M��N�ֱ�ΪA1C1��B1C���е㣬�Ҳ���ABB1A1�͵���ABC��
��ͼ����֪б������ABC-A1B1C1�������ⳤ��Ϊ2����B1BA=$\frac{��}{3}$��M��N�ֱ�ΪA1C1��B1C���е㣬�Ҳ���ABB1A1�͵���ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
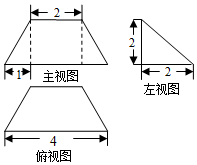
| A�� | 4 | B�� | $\frac{16}{3}$ | C�� | $\frac{20}{3}$ | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | ��0��$\frac{2}{3}$�� | C�� | [$\frac{3}{8}$��$\frac{2}{3}$�� | D�� | [$\frac{3}{8}$��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com