
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析 (1)从频数分布表算出女性用户中“认可”手机人数与“不认可”手机人数,填入表格即可;
同理算出男性用户中“认可”手机人数与“不认可”手机人数,填入表格,可得2×2列联表,
由公式计算出K2的值与临界值中数据比较即可;
(2)评分不低于80分有6人,其中评分小于90分的人数为4,记为A、B、C、D,
评分不小于90分的人数为2,记为a、b,
写出从6人中任取2人的所有基本事件,从中找出两名用户评分都小于90分的基本事件,即可求其概率.
解答 解:(1)由频数分布表可得2×2列联表如下图:
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
点评 本题考查了对立性检验和古典概型的概率计算问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
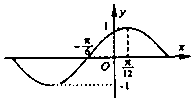
| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=cos({2x-\frac{π}{6}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({4x-\frac{π}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
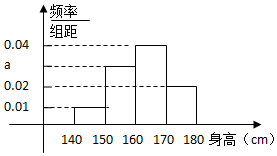 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com