
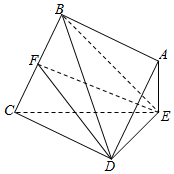
 已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$
已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$分析 (I)根据面面垂直的判定定理证明平面ABCD⊥平面ADE即可
(Ⅱ)建立空间坐标系,利用向量法求出平面的法向量,利用向量法结合二面角的余弦值求出F的位置即可得到结论.
解答  (Ⅰ)证明:∵AE⊥平面CDE,
(Ⅰ)证明:∵AE⊥平面CDE,
∴AE⊥平面DE,AE⊥CD,
∵AE=1,AD=2,∴DE=$\sqrt{3}$,
∵CE=$\sqrt{7}$,CD=2,
∴CD2+DE2=3+4=7,即CD2+DE2=CE2,
∴△CDE是直角三角形,
则CD⊥DE,
∵DE∩AE=E,
∴CD⊥平面ADE;
∵CD?平面ABCD.
∴平面ABCD⊥平面ADE;
(Ⅱ)建立以D为坐标原点,DC,ED,垂直于平面CDE的直线分别为x,y,z轴的空间直角坐标系如图:
则A(0,-$\sqrt{3}$,1),E(0,-$\sqrt{3}$,0),C(2,0,0),D(0,0,0),B(2,-$\sqrt{3}$,1),
设$\overrightarrow{CF}$=t$\overrightarrow{CB}$=t(0,-$\sqrt{3}$,1)=(0,-$\sqrt{3}$t,t)(0≤t≤2),
则$\overrightarrow{DF}$=$\overrightarrow{DC}$+$\overrightarrow{CF}$=(2,0,0)+(0,-$\sqrt{3}$t,t)=(2,-$\sqrt{3}$t,t),
$\overrightarrow{DE}$=(0,-$\sqrt{3}$,0),
则设平面DEF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DF}=0}\\{\overrightarrow{n}•\overrightarrow{DE}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x-\sqrt{3}ty+tz=0}\\{-\sqrt{3}y=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x+tz=0}\\{y=0}\end{array}\right.$,
令z=1,则x=-$\frac{t}{2}$,y=0,
即为$\overrightarrow{n}$=(-$\frac{t}{2}$,0,1),
平面AED的法向量为$\overrightarrow{m}$=(1,0,0),
若二面角A-DE-F的余弦值为$\frac{\sqrt{37}}{37}$,
则|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=$\frac{|-\frac{t}{2}|}{\sqrt{(-\frac{t}{2})^{2}+1}}$=$\frac{\sqrt{37}}{37}$,
平方得$\frac{\frac{{t}^{2}}{4}}{\frac{{t}^{2}}{4}+1}=\frac{1}{37}$,即9t2=1,则t2=$\frac{1}{9}$,
则t=$\frac{1}{3}$,
即CF=$\frac{1}{3}$CB=$\frac{2}{3}$,
即点F在BC上的位置满足CF=$\frac{2}{3}$,即可满足条件.
点评 本题主要考查面面垂直判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
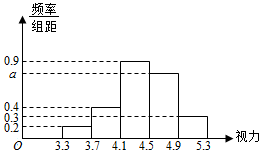 某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.
某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
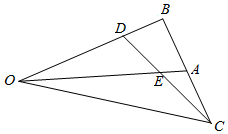 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
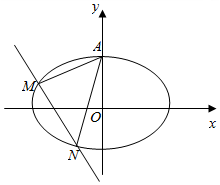 过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.
过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com