
分析 由题意可得x+y=($\frac{4}{x}+\frac{9}{y}$)(x+y)=13+$\frac{4y}{x}$+$\frac{9x}{y}$,由基本不等式可得.
解答 解:∵$\frac{4}{x}+\frac{9}{y}$=1,且x>0,y>0,
∴x+y=($\frac{4}{x}+\frac{9}{y}$)(x+y)
=13+$\frac{4y}{x}$+$\frac{9x}{y}$≥13+2$\sqrt{\frac{4y}{x}•\frac{9x}{y}}$=25
当且仅当$\frac{4y}{x}$=$\frac{9x}{y}$即x=10且y=15时取等号.
故选答案为:25.
点评 本题考查基本不等式求最值,“1”的整体代换是解决问题的关键,属基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015-2016学年四川成都石室中学高二文下期中数学试卷(解析版) 题型:解答题
在四棱锥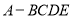 中, 底面
中, 底面 为菱形,侧面
为菱形,侧面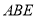 为等边三角形,且侧面
为等边三角形,且侧面 底面
底面 ,
,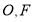 分别为
分别为 的中点.
的中点.

(1)求证: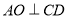 ;
;
(2)求证: 平面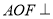 平面
平面 ;
;
(3)侧棱 上是否存在点
上是否存在点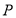 ,使得
,使得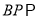 平面
平面 ?若存在,求出
?若存在,求出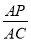 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$|sinx| | B. | $y=\frac{1}{2}cos(2x+\frac{π}{2})$ | C. | y=tanx | D. | y=cos$\frac{1}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com