
分析 (1)根据绝对值不等式的解法,求解即可.
(2)求出m+n=2,利用1的代换,结合基本不等式求$\frac{{{m^2}+2}}{m}+\frac{{{n^2}+1}}{n}$的最小值.
解答 解:(1)由f(x)<2知|2x-1|<2,
于是-2<2x-1<2,
解得$-\frac{1}{2}<x<\frac{3}{2}$,
故不等式f(x)<2的解集为$(-\frac{1}{2},\frac{3}{2})$.
(2)由条件得g(x)=|2x-1|+|2x-3|≥|2x-1-(2x-3)|=2,
当且仅当$x∈[\frac{1}{2},\frac{3}{2}]$时,其最小值a=2,
即m+n=2.
又$\frac{2}{m}+\frac{1}{n}=\frac{1}{2}(m+n)(\frac{2}{m}+\frac{1}{n})=\frac{1}{2}(3+\frac{2n}{m}+\frac{m}{n})≥\frac{1}{2}(3+2\sqrt{2})$,
所以$\frac{{{m^2}+2}}{m}+\frac{{{n^2}+1}}{n}=m+n+\frac{2}{m}+\frac{1}{n}≥2+\frac{1}{2}(3+2\sqrt{2})=\frac{{7+2\sqrt{2}}}{2}$,
故$\frac{{{m^2}+2}}{m}+\frac{{{n^2}+1}}{n}$的最小值为$\frac{{7+2\sqrt{2}}}{2}$,
此时$m=4-2\sqrt{2}$,$n=2\sqrt{2}-2$.
点评 本题主要考查绝对值不等式的解法,以及不等式恒成立问题,利用1的代换结合基本不等式,将不等式恒成立进行转化求解是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
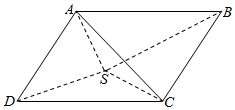 如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.
如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
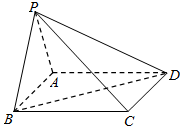 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,面PAB⊥底面ABCD,PB=1,且∠PBA=60°
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,面PAB⊥底面ABCD,PB=1,且∠PBA=60°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
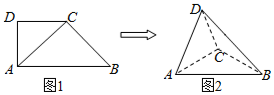 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到如图2所示的几何体D-ABC
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到如图2所示的几何体D-ABC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | θ=$\frac{π}{4}$(ρ∈R) | B. | θ=$\frac{5π}{4}$(ρ≤0) | C. | θ=$\frac{5π}{4}$(ρ∈R) | D. | θ=$\frac{π}{4}$(ρ≤0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com