
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 通过当x∈[4,+∞)时,f(x)∈[16,+∞),即可判断①的正误.
f(x)=$\frac{sinx}{x}$,随着x的增大,函数值趋近于0,判断函数f(x)在[4,+∞)内有一个宽度为1的通道,判断②的正误.
对于③,当x∈[4,+∞)时,确定函数的值域,2x≥16,即可判断③的正误;
对于④,当x∈[1,+∞)时,f(x)=$\sqrt{{x}^{2}-1}$,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,可取另一直线,满足在[4,+∞)有一个宽度为1的通道;
解答 解:对于①,当x∈[1,+∞)时,f(x)∈[1,+∞),故在[1,+∞)不存在一个宽度为1的通道;∴①不正确.
对于②,f(x)=$\frac{sinx}{x}$,随着x的增大,函数值趋近于0,对于任意给定的正数x,都存在一个实数4,使得函数f(x)在[4,+∞)内有一个宽度为1的通道,故f(x)在正无穷处有永恒通道;∴②正确.
对于③,当x∈[4,+∞)时,2x≥16,故在[4,+∞)没有一个宽度为1的通道,∴③不正确.
对于④,当x∈[4,+∞)时,f(x)=$\sqrt{{x}^{2}-1}$,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为y=x-1,满足在[4,+∞)有一个宽度为1的通道;∴④正确.
故选:C.
点评 本题考查的重点是对新定义的理解,解题的关键是通过研究函数的性质,找出满足题意的直线.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
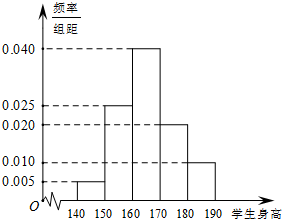 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com