
分析 (1)先用数学归纳法证明0<an<1,n∈N*.又由0<an<1,得an+1-an=an-ln(1+an)-an=-ln(1+an)<0,从而an+1<an;
(2)利用累乘法即可证明.
解答 证明:(1)先用数学归纳法证明0<an<1.
①当n=1时,由已知得结论成立
②假设n=k(k∈N+)时0<ak<1成立,则当n=k+1时,设f(x)=x-ln(x+1),
于是f′(x)=1-$\frac{1}{x+1}$在(0,1)上恒有f′(x)>0,所以f(x)在(0,1)上递增,
∴f(0)<f(ak)<f(1)=1-ln2<1,又f(0)=0,从而0<ak+1<1,
这就是说当n=k+1时命题成立,
由①②知0<an<1成立
又an+1-an=-ln(1+an)<0,即an+1<an,
综上可得,0<an+1<an<1,n∈N+.
(2)∵an+1<$\frac{{a}_{n}^{2}}{2}$,
∴$\frac{{a}_{n+1}}{{a}_{n}}$<$\frac{{a}_{n}}{2}$,
从而当n≥2时,$\frac{{a}_{n}}{{a}_{1}}$=$\frac{{a}_{2}}{{a}_{1}}$×$\frac{{a}_{3}}{{a}_{2}}$×…×$\frac{{a}_{n}}{{a}_{n-1}}$<$\frac{{a}_{1}}{2}$×$\frac{{a}_{2}}{2}$×…×$\frac{{a}_{n-1}}{2}$,
∵a1=$\frac{\sqrt{2}}{2}$,0<an+1<an<1;
∴an<$\frac{{a}_{1}}{2}$×$\frac{{a}_{2}}{2}$×…×$\frac{{a}_{n-1}}{2}$•a1=$\frac{{a}_{1}^{2}}{{2}^{n-1}}$=$\frac{1}{{2}^{n}}$
点评 本题主要考查数列与函数,不等式的综合运用,主要涉及了数学归纳法,导数法,累乘法等常用解题方法,综合性强,要求思路要清,意志力要强.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{2}$-1 | C. | 2$\sqrt{2}$-2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
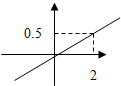 某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com