
 时,若不等式f′(x)>-
时,若不等式f′(x)>- 对任意x∈R恒成立,求b的取值范围;
对任意x∈R恒成立,求b的取值范围; t在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.
t在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围. 时,f′(x)=x2+2bx+b-
时,f′(x)=x2+2bx+b- ,…(1分)
,…(1分)
 )=
)=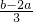 .
. )•f′(-1)<0,故结论成立.
)•f′(-1)<0,故结论成立. )(x+
)(x+ )
) ),(
),(  ,+∞)上是増函数,
,+∞)上是増函数, ,
, ]上是减函数,由f(x)=0解得x=±1,x=0,
]上是减函数,由f(x)=0解得x=±1,x=0, 时,f(t)≥-
时,f(t)≥- t≥0,即t3-t≥-
t≥0,即t3-t≥- ,解得-
,解得- ≤t≤0或t≥-
≤t≤0或t≥- ;
; <t<0时,f(t)>-
<t<0时,f(t)>- t≥0,解得-
t≥0,解得- <t<0;
<t<0; 时,f(t)≤-
时,f(t)≤- t<0,即t3-t≤-
t<0,即t3-t≤- ,解得0<t≤
,解得0<t≤ ;
; 时,f(t)<-
时,f(t)<- t<0,故
t<0,故  <t<
<t< .
. =f(
=f( )∴t=
)∴t= .
. ≤t<0或0<t<
≤t<0或0<t< 或t=
或t= .
. 时,f′(x)=x2+2bx+b-
时,f′(x)=x2+2bx+b- ,依题意 f′(x)>-
,依题意 f′(x)>- 即x2+2bx+b>0恒成立,由二次函数的性质,分类讨论可得答案;
即x2+2bx+b>0恒成立,由二次函数的性质,分类讨论可得答案; )=
)=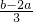 .再由a,b不同时为零,所以f′(-
.再由a,b不同时为零,所以f′(- )•f′(-1)<0,故结论成立;
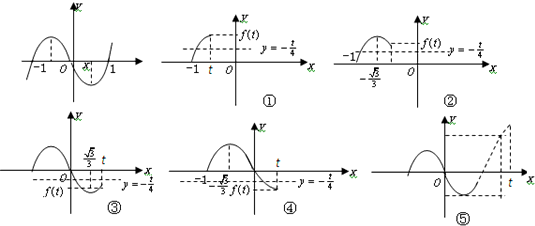
)•f′(-1)<0,故结论成立; t在[-1,t](t>-1)上有且只有一个实数根”转化为“函数f(x)与y=-
t在[-1,t](t>-1)上有且只有一个实数根”转化为“函数f(x)与y=- t的交点”问题解决,先求函数f(x)因为f(x)=ax3+bx2+(b-a)x为奇函数,可解得b=0,所以f(x)=ax3-ax,再由“f(x)在x=1处的切线垂直于直线x+2y-3=0”解得a,从而得到f(x),再求导,由f′(x)=3(x-
t的交点”问题解决,先求函数f(x)因为f(x)=ax3+bx2+(b-a)x为奇函数,可解得b=0,所以f(x)=ax3-ax,再由“f(x)在x=1处的切线垂直于直线x+2y-3=0”解得a,从而得到f(x),再求导,由f′(x)=3(x- )(x+
)(x+ ),知f(x(-∞,-
),知f(x(-∞,- ),(
),(  ,+∞)上是増函数,在[-
,+∞)上是増函数,在[- ,
, ]上是减函数,明确函数的变化规律,再研究两个函数的相对位置求解.
]上是减函数,明确函数的变化规律,再研究两个函数的相对位置求解.

科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com