
| 分组 | 频数 | 频率 |
| [0,10) | 0.05 | |
| [10,20) | 0.10 | |
| [20,30) | 30 | |
| [30,40) | 0.25 | |
| [40,50) | 0.15 | |
| [50,60] | 15 | |
| 合计 | n | 1 |
分析 (1)频数等于45时频率为0.45,由此能求出n的值和月均用电量的平均数估计值.
(2)用电量小于30度的居民共有50位,用分层抽样的方法从用电量小于30度的居民中抽取5位居民,则第一组抽1人,第二组抽1人,第三组抽3人,从这5位居民中选2人,共有10种选法,由此能求出至少有1位居民月均用电量在20至30度的概率.
解答 解:(1)∵频数等于45时频率为0.45,
∴$n=\frac{45}{0.45}=100$(2分)
月均用电量的平均数:
$\overline x=5×0.1+15×0.1+25×0.3+35×0.2+45×0.15+55×0.15=31.5$(6分)
(2)用电量小于30度的居民共有50位,用分层抽样的方法从用电量小于30度的居民中抽取5位居民,
则第一组抽1人,第二组抽1人,第三组抽3人(8分)
从这5位居民中选2人,共有10种选法,
至少有1位居民月均用电量在20至30度的共有9种,(10分)
至少有1位居民月均用电量在20至30度的概率是$\frac{9}{10}$.(12分)
点评 本题考查频率分布表的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
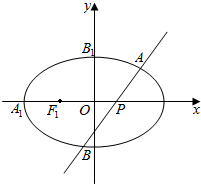 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15,20,25 | B. | 2,4,8,16,32 | C. | 5,6,7,8,9 | D. | 6,16,26,36,46 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<1<b | B. | a<b<1 | C. | 1<a<b | D. | b<1<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (1,2)∪(2,+∞) | D. | (1,3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com