
分析 连接BD,在△ABD和△BCD中分别由余弦定理可得5cosA-6cosC=1,由面积可得5sinA+6sinC=S,将2式子平方后相加解三角函数的值域可得S的不等式,解不等式可得答案.
解答 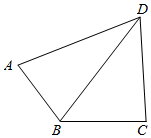 解:连接BD,在△ABD和△BCD中分别应用余弦定理,
解:连接BD,在△ABD和△BCD中分别应用余弦定理,
可得:BD2=AB2+AD2-2AB•AD•cosA=BC2+CD2-2BC•CD•cosC,
整理有:5cosA-6cosC=1…①?,
四边形ABCD的面积:$S={S_{△ABD}}+{S_{△BCD}}=\frac{1}{2}AB•AD•sinA+\frac{1}{2}BC•CD•sinC=5sinA+6sinC$,…②?
?①式②?式平方相加得:S2+1=25-60cos(A+C)+36,
可得:S2=60-60cos(A+C)≤120,
当A+C=π时,四边形ABCD的面积S取到最大值为$2\sqrt{30}$.
故答案为:$2\sqrt{30}$.
点评 本题考查解三角形,涉及余弦定理和三角形的面积公式以及不等式的性质,属中档题.


科目:高中数学 来源: 题型:填空题
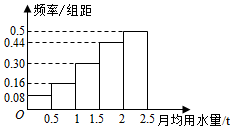 如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨.
如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,-2,-1,0} | B. | {-2,-1,0} | C. | {-3,-2,-1,0,1} | D. | {-2,-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 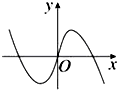 | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com