
已知向量a="(cos" α,sin α),b="(cos" β,sin β),0<β<α<π.
(1)若|a-b|=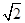 ,求证:a⊥b;
,求证:a⊥b;
(2)设c=(0,1),若a+b=c,求α,β的值.
科目:高中数学 来源: 题型:填空题
设 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射 ,记
,记 的象为
的象为 。若映射
。若映射 满足:对所有
满足:对所有 及任意实数
及任意实数 都有
都有 ,则
,则 称为平面
称为平面 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设 是平面
是平面 上的线性变换,
上的线性变换, ,则
,则 ;
;
②若 是平面
是平面 上的单位向量,对
上的单位向量,对 ,则
,则 是平面
是平面 上的线性变换;
上的线性变换;
③对 ,则
,则 是平面
是平面 上的线性变换;
上的线性变换;
④设 是平面
是平面 上的线性变换,
上的线性变换,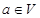 ,则对任意实数
,则对任意实数 均有
均有 。
。
其中的真命题是 .(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知点A(2,3),B(5,4),C(7,10),若 =
= +λ·
+λ· (λ∈R),试问:
(λ∈R),试问:
(1) λ为何值时,点P在第一、三象限角平分线上;
(2) λ为何值时,点P在第三象限.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com