
(本小题满分12分)兰州市为增强市民的环保意识,面向全市征召宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组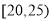 ,第2组
,第2组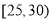 ,第3组
,第3组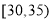 ,第4组
,第4组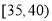 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
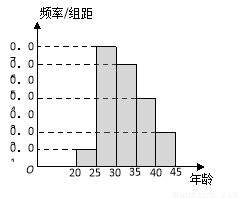
(Ⅰ)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从
第3,4,5组各抽取多少名志愿者?
(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4
组至少有一名志愿者被抽中的概率.
(1)3人,2人,1人;(2)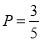 .
.
【解析】
试题分析:(1)解决频率分布直方图的问题,关键在于找出图中数据之间的关系,这些数据中,比较明显的有组距、 ,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
试题解析:(Ⅰ)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组: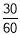 ×6=3;
×6=3;
第4组: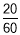 ×6=2;
×6=2;
第5组: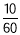 ×6=1;
×6=1;
即应从第3,4,5组中分别抽取3人,2人,1人. 6分
(Ⅱ)记第3组的3名志愿者为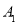 ,
,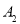 ,
,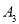 ,第4组的2名志愿者为
,第4组的2名志愿者为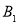 ,
, ,第5组的1名志愿者为
,第5组的1名志愿者为 .则从6名志愿者中抽取2名志愿者有:
.则从6名志愿者中抽取2名志愿者有:
(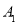 ,
,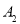 ), (
), (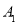 ,
,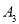 ),(
),(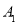 ,
,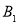 ),(
),(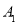 ,
, ),(
),(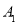 ,
, ),
),
(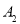 ,
,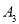 ),(
),(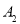
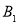 ),(
),(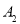 ,
, ), (
), (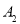 ,
, ),
),
(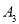 ,
,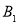 ),
), 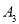 ,
, ), (
), (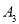 ,
, ),
),
(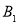 ,
, ),(
),(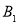 ,
, ),(
),( ,
, ),共有15种.
),共有15种.
其中第4组的2名志愿者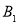 ,
, 至少有一名志愿者被抽中的有:
至少有一名志愿者被抽中的有:
(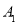 ,
,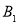 ),(
),(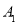 ,
, ),(
),(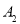
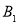 ),(
),(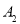 ,
, ), (
), (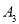 ,
,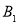 ), (
), (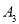 ,
, ),(
),(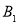 ,
, ),
),
(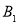 ,
, ),(
),( ,
, ),共有9种, 10分
),共有9种, 10分
所以第4组至少有一名志愿者被抽中的概率为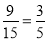 12分
12分
考点:1、频率分布直方图的应用;2、利用古典概型求随机事件的概率 .
考点分析: 考点1:古典概率 试题属性

科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
在复平面内,复数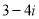 ,
,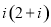 对应的点分别为
对应的点分别为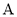 ,
,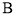 ,则线段
,则线段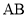 的中点
的中点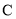 对应的复数为( )
对应的复数为( )
A.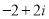 B.
B.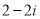 C.
C. D.
D.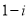
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知等差数列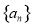 的前
的前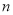 项和为
项和为 ,又知
,又知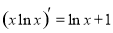 ,且
,且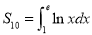 ,
,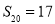 ,则
,则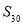 为( )
为( )
A.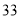 B.
B.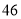 C.
C.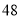 D.
D.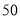
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)若不等式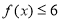 的解集为
的解集为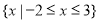 ,求实数
,求实数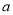 的值;
的值;
(2)在(1)的条件下,若存在实数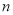 使
使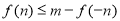 成立,求实数
成立,求实数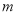 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试理科数学试卷(解析版) 题型:填空题
椭圆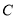 的中心在原点,焦点在
的中心在原点,焦点在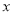 轴上,若椭圆
轴上,若椭圆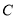 的离心率等于
的离心率等于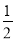 ,且它的一个顶点恰好是抛物线
,且它的一个顶点恰好是抛物线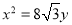 的焦点,则椭圆
的焦点,则椭圆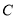 的标准方程为 .
的标准方程为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)求证:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com