
(本小题满分12分)已知函数
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)求证:

(1)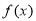 的单调递减区间为
的单调递减区间为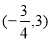 ;(2)
;(2)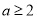 ;(3)证明见解析
;(3)证明见解析
【解析】
试题分析:(1)函数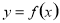 在某个区间内可导,则若
在某个区间内可导,则若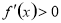 ,则
,则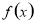 在这个区间内单调递增,若
在这个区间内单调递增,若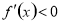 ,则
,则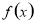 在这个区间内单调递减;(2)对于恒成立的问题,常用到两个结论:(1)
在这个区间内单调递减;(2)对于恒成立的问题,常用到两个结论:(1)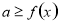 恒成立
恒成立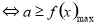 ,(2)
,(2) 恒成立
恒成立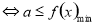 ;(3)利用导数方法证明不等式
;(3)利用导数方法证明不等式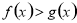 在区间
在区间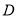 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数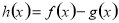 ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数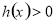 ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数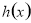 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
试题解析:(1) 当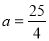 时
时 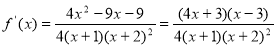
由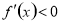 ,得
,得

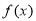 的单调递减区间为
的单调递减区间为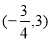 4分
4分
(2) 由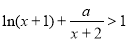 得
得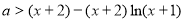
记
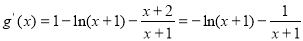
当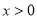 时
时 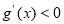

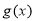 在
在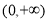 递减
递减
又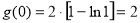

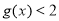
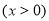

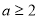 8分
8分
(3)由(Ⅱ)知 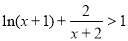
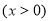

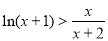
取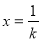 得
得 即
即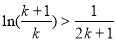

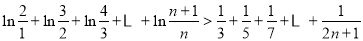 12分
12分
考点:1、利用导数求函数的单调区间;2、恒成立的问题;3、证明不等式.
考点分析: 考点1:导数及其应用 试题属性

科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)兰州市为增强市民的环保意识,面向全市征召宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组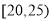 ,第2组
,第2组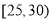 ,第3组
,第3组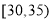 ,第4组
,第4组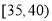 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
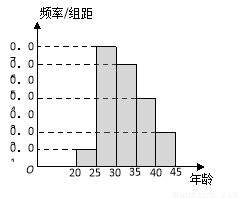
(Ⅰ)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从
第3,4,5组各抽取多少名志愿者?
(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4
组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:选择题
已知函数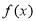 的定义域为
的定义域为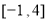 ,部分对应值如下表,
,部分对应值如下表,

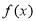 的导函数
的导函数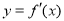 的图象如右图所示.当
的图象如右图所示.当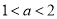 时,函数
时,函数 的零点的个数为( )
的零点的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:选择题
下面是关于复数 的四个命题:
的四个命题:
 :
: ,
, 

 的共轭复数为
的共轭复数为
 的虚部为
的虚部为
其中真命题为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:填空题
在平面直角坐标系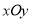 中,圆
中,圆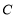 的方程为
的方程为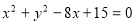 ,若直线
,若直线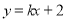 上至少存在一点,使得以该点为圆心,半径为
上至少存在一点,使得以该点为圆心,半径为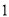 的圆与圆
的圆与圆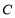 有公共点,则
有公共点,则 的最小值是____.
的最小值是____.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:选择题
定义行列式运算: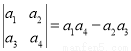 .若将函数
.若将函数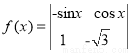 的图象向左平移
的图象向左平移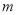
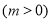 个单位后,所得图象对应的函数为奇函数,则
个单位后,所得图象对应的函数为奇函数,则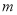 的最小值是( )
的最小值是( )
A.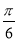 B.
B.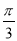 C.
C. D.
D.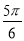
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题13分)平面内给定三个向量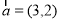 ,
,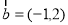 ,
,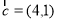 .
.
(Ⅰ)设向量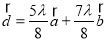 ,且
,且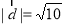 ,求向量
,求向量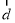 的坐标;
的坐标;
(Ⅱ)若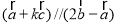 ,求实数k的值.
,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com