
分析 (1)通过Sn=2an-2与Sn-1=2an-1-2(n≥2)作差,进而可得数列{an}是首项、公比均为2的等比数列;
(2)通过(1)裂项可知bn=4($\frac{1}{n}$-$\frac{1}{n+1}$),进而并项相加即得结论.
解答 (1)证明:依题意,Sn=2an-2,
∴Sn-1=2an-1-2(n≥2),
两式相减得:an=2an-2an-1,即an=2an-1,
又∵a1=2a1-2,即a1=2,
∴数列{an}是首项、公比均为2的等比数列;
(2)解:由(1)可知an=2n,
∴bn=$\frac{1}{lo{g}_{4}{a}_{n}•lo{g}_{4}{a}_{n+1}}$=$\frac{1}{\frac{n}{2}•\frac{n+1}{2}}$=$\frac{4}{n(n+1)}$=4($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=4(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=4(1-$\frac{1}{n+1}$)
=$\frac{4n}{n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
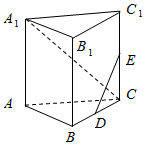 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{8}$ | B. | 4 | C. | $\frac{40}{27}$ | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com