
分析 (1)利用斜率共线,直接求解即可.
(2)利用斜率的数量积列出不等式,即可求出结果.
(3)利用斜率的垂直条件,列出方程求解即可.
解答 解:(1)向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,1),$\overrightarrow{a}$∥$\overrightarrow{b}$,
可得2x=1,
∴x=$\frac{1}{2}$
(2)若<$\overrightarrow{a}$,$\overrightarrow{b}$>为锐角,则$\overrightarrow{a}$•$\overrightarrow{b}$>0且$\overrightarrow{a}$,$\overrightarrow{b}$不同向.
$\overrightarrow{a}$•$\overrightarrow{b}$=x+2>0,∴x>-2,当x=$\frac{1}{2}$时,$\overrightarrow{a}$,$\overrightarrow{b}$同向.
∴x>-2且x≠$\frac{1}{2}$.
(3)$\overrightarrow{a}$+2$\overrightarrow{b}$=(1+2x,4),2$\overrightarrow{a}$-$\overrightarrow{b}$=(2-x,3),($\overrightarrow{a}$+2$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),
可得(2x+1)(2-x)+3×4=0.
即-2x2+3x+14=0.
解得:x=$\frac{7}{2}$或x=-2.
点评 本题考查斜率的数量积的应用,斜率共线以及斜率垂直条件的应用,考查计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
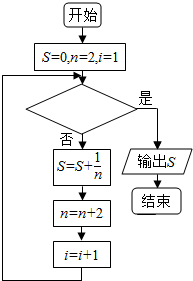 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i≥49? | B. | i≥50? | C. | i≥51? | D. | i≥100? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-2 | B. | $y={(\sqrt{x-2})^2}$ | C. | $y=\frac{1}{{\sqrt{x-2}}}$ | D. | $y=\sqrt{{{(x-2)}^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com