Question

3．运行如图所示的程序框图后，输出的m值是（　　）

• A． -3
• B． $-\frac{1}{2}$
• C． $\frac{1}{3}$
• D． 2

Answer 1

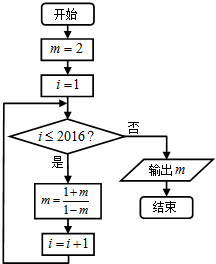
分析 模拟执行程序，依次写出前几次循环得到的m，i的值，观察规律可知，m的取值周期为4，由于2016=504×4，可得当i=2017时不满足条件i≤2016，退出循环，输出m的值为2．

解答 解：模拟执行程序，可得
m=2，i=1
满足条件i≤2016，m=-3，i=2
满足条件i≤2016，m=-$\frac{1}{2}$，i=3
满足条件i≤2016，m=$\frac{1}{3}$，i=4
满足条件i≤2016，m=2，i=5
…
观察规律可知，m的取值周期为4，由于2016=504×4，可得
满足条件i≤2016，m=$\frac{1}{3}$，i=2016
满足条件i≤2016，m=2，i=2017
不满足条件i≤2016，退出循环，输出m的值为2．
故选：D．

点评 本题主要考查了循环结构的程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．