Question

12．已知函数y=|x|+$\frac{1}{|x-1|}$
（I）求f（x）的最小值；
（Ⅱ）方程f（x）-m=0有几个解．

Answer 1

分析 （I）根据绝对值不等式的性质，分别进行讨论，结合函数的单调性以及基本不等式进行求解即可求f（x）的最小值；
（Ⅱ）根据（Ⅰ）的条件，作出函数f（x）的图象，利用数形结合即可求方程f（x）-m=0有几个解．

解答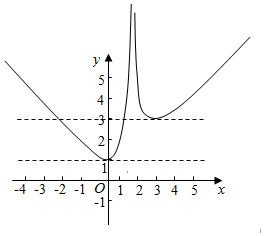
解：（I）当x＞1时，f（x）=x+$\frac{1}{x-1}$=x-1+$\frac{1}{x-1}$+1≥2$\sqrt{（x-1）•\frac{1}{x-1}}$+1=2+1=3，当且仅当x-1=$\frac{1}{x-1}$，即x-1=1，x=2时取等号；
当x≤0时，f（x）=-x-$\frac{1}{x-1}$=-x+1-$\frac{1}{x-1}$-1=（1-x）+$\frac{1}{1-x}$-1≥2$\sqrt{（1-x）•\frac{1}{1-x}}$-1=2-1=1，当且仅当1-x=-$\frac{1}{x-1}$，即1-x=1，x=0时取等号；
当0＜x＜1时，f（x）=x-$\frac{1}{x-1}$，则函数f（x）为增函数，
当x=0时，f（0）=1，当x→1时，→+∞，即此时f（x）＞1
综上函数的f（x）的最小值是1；
（Ⅱ）由方程f（x）-m=0的f（x）=m，
由（Ⅰ）作出函数f（x）的图象如图，
则当m＜1时，f（x）=m无解，
当m=1时，f（x）=m有1个解，
当1＜m＜3时，f（x）=m有2个解
当m=3时，f（x）=m有3个解，
当m＞3时，f（x）=m有4个解．

点评 本题主要考查函数与方程的应用，根据绝对值的应用进行分类讨论，利用数形结合以及基本不等式的性质是解决本题的关键．综合性较强，难度较大．