练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】用简单随机抽样方法从含有6个个体的总体中，抽取一个容量为2的样本，某一个体a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是
    ．

    【答案】 ， ，
    【解析】解：从含有6个个体的总体中，抽取一个容量为2的样本，
    在整个抽样过程中被抽到的概率是= ，
    一个体a第一次被抽到，表示从6个个体中抽一个个体，
    被抽到的概率是 ，
    第二次被抽到表示第一次未被抽到且第二次抽到，
    这是一个相互独立事件的概率，
    根据相互独立事件同时发生的概率知P=，
    所以答案是：；；
    【考点精析】利用相互独立事件对题目进行判断即可得到答案，需要熟知事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）的上、下两个焦点分别为， ，过的直线交椭圆于， 两点，且的周长为8，椭圆的离心率为.

    （1）求椭圆的标准方程；

    （2）已知为坐标原点，直线： 与椭圆有且仅有一个公共点，点， 是直线上的两点，且， ，求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={（x，y）|x2+（y+1）2≤1}，B={（x，y）| x+y=4m}，命题P：A∩B=，命题q：直线 + =1在两坐标轴上的截距为正．
    （1）若命题P为真命题，求实数m的取值范围；
    （2）若“p∨q”为真，“p∧q”为假，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂的A、B、C三个不同车间生产同一产品的数量（单位：件）如表所示．质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测．

    车间

    A

    B

    C

    数量

    50

    150

    100

    （1）求这6件样品中来自A、B、C各车间产品的数量；
    （2）若在这6件样品中随机抽取2件进行进一步检测，求这2件商品来自相同车间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥CD，∠ABC=90°，且CD=2，AB=BC=PA=1，PD= ．
    （1）求三棱锥A﹣PCD的体积；
    （2）问：棱PB上是否存在点E，使得PD∥平面ACE？若存在，求出 的值，并加以证明；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒中装有各色球12只，其中5个红球，4个黑球，2个白球，1个绿球；从中随机取出1球．求：
    （1）取出的1球是红球或黑球的概率；
    （2）取出的1球是红球或黑球或白球的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体ABCD﹣A1B1C1D1中，点M是平面A1B1C1D1内一点，且BM∥平面ACD1 ， 则tan∠DMD1的最大值为（ ）

    A.
    B.1
    C.2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图△ABC是等腰三角形，BA=BC，DC⊥平面ABC，AE∥DC，若AC=2且BE⊥AD，则（ ）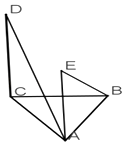

    A.AB+BC有最大值
    B.AB+BC有最小值
    C.AE+DC有最大值
    D.AE+DC有最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中，E、F、G分别是CB．CD．CC1的中点．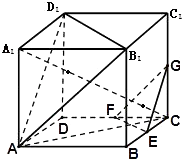

    （1）求直线 A1C与平面ABCD所成角的正弦的值；
    （2）求证：平面A B1D1∥平面EFG．

    查看答案和解析>>

    同步练习册答案