练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

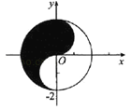
    【题目】太极图被称为“中华第一图”．从孔庙大成殿梁柱，到楼观台、三茅宫标记物；从道袍、卦摊、中医、气功、武术到韩国国旗，太极图无不跃居其上．这种广为人知的太极图，其形状如阴阳两鱼互抱在一起，因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中，阴影部分可表示为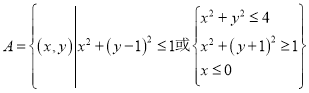，设点，则的最大值与最小值之差是（ ）

    A.B.C.D.

    【答案】C

    【解析】

    平移直线，当直线与圆切于第三象限的点时，该直线在轴上的截距最小，当直线与圆相切于第一象限的点时，该直线在轴上的截距最大，利用圆心到直线的距离等于圆的半径求出对应的值，即可得出所求结果.

    如下图所示：

    当直线与圆切于第三象限的点时，该直线在轴上的截距最小，

    此时，由题意得，解得，此时；

    当直线与圆相切于第一象限的点时，该直线在轴上的截距最大，此时，由题意可得，解得，此时.

    因此，的最大值与最小值之差是.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】东莞的轻轨给市民出行带来了很大的方便，越来越多的市民选择乘坐轻轨出行，很多市民都会开汽车到离家最近的轻轨站，将车停放在轻轨站停车场，然后进站乘轻轨出行，这给轻轨站停车场带来很大的压力．某轻轨站停车场为了解决这个问题，决定对机动车停车施行收费制度，收费标准如下：4小时内（含4小时）每辆每次收费5元；超过4小时不超过6小时，每增加一小时收费增加3元；超过6小时不超过8小时，每增加一小时收费增加4元，超过8小时至24小时内（含24小时）收费30元；超过24小时，按前述标准重新计费．上述标准不足一小时的按一小时计费．为了调查该停车场一天的收费情况，现统计1000辆车的停留时间（假设每辆车一天内在该停车场仅停车一次），得到下面的频数分布表：

    （小时）

    频数（车次）

    100

    100

    200

    200

    350

    50

    以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率．

    （1）现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研，记录并统计了停车时长与司机性别的列联表：

    男

    女

    合计

    不超过6小时

    30

    6小时以上

    20

    合计

    100

    完成上述列联表，并判断能否有90%的把握认为“停车是否超过6小时”与性别有关？

    （2）（i）表示某辆车一天之内（含一天）在该停车场停车一次所交费用，求的概率分布列及期望；

    （ii）现随机抽取该停车场内停放的3辆车，表示3辆车中停车费用大于的车辆数，求的概率．

    参考公式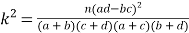：，其中

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.780

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．

    （1）求1名顾客摸球2次停止摸奖的概率；

    （2）记为1名顾客5次摸奖获得的奖金数额，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(本小题满分12分)

    已知函数（其中a是实数）．

    （1）求的单调区间；

    （2）若设，且有两个极值点 ，求取值范围．（其中e为自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一研学实践活动小组利用课余时间，对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查，月销售单价（单位：元）和月销售量（单位：百件）之间的一组数据如下表所示：

    月份

    1

    2

    3

    4

    5

    月销售单价（元）

    1.6

    1.8

    2

    2.2

    2.4

    月销售量（百件）

    10

    8

    7

    6

    4

    （1）根据1至5月份的数据，求出关于的回归直线方程；

    （2）预计在今后的销售中，月销售量与月销售单价仍然服从（1）中的关系，若该种产品的成本是1元/件，那么该产品的月销售单价应定为多少元才能获得最大月利润？（注：利润=销售收入-成本）

    （回归直线方程，其中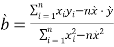.参考数据：，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲、乙两地生产同一种瓷器，现从两地的瓷器中随机抽取了一共300件统计质量指标值，得到如图的两个统计图，其中甲地瓷器的质量指标值在区间和的频数相等.

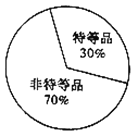
    甲地瓷器质量频率分布直方图 乙地瓷器质量扇形统计图

    （1）求直方图中的值，并估计甲地瓷器质量指标值的平均值；（同一组中的数据用区间的中点值作代表）

    （2）规定该种瓷器的质量指标值不低于125为特等品，且已知样本中甲地的特等品比乙地的特等品多10个，结合乙地瓷器质量扇形统计图完成下面的列联表，并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异？

    物等品

    非特等品

    合计

    甲地

    乙地

    合计

    附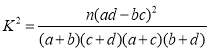：，其中.

    0.10

    0.05

    0.025

    0.01

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有六名百米运动员参加比赛，甲、乙、丙、丁四名同学猜测谁跑了第一名.甲猜不是就是;乙猜不是;丙猜不是中任一个；丁猜是中之一，若四名同学中只有一名同学猜对，则猜对的是（ ）

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数f（x）的单调递增区间；

    （2）将函数f（x）的图象向右平移个单位，再将所得图象的橫坐标缩短到原来的一半，纵坐标不变，得到新的函数y＝g（x），当时，求g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线l的参数方程为（t为参数，0）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为．

    (Ⅰ)写出曲线C的直角坐标方程；

    (Ⅱ)若直线l与曲线C交于A，B两点，且AB的长度为2，求直线l的普通方程．

    查看答案和解析>>

    同步练习册答案