
分析 根据对数的运算法则进行化简,转化为一元二次方程,讨论a的取值范围进行求解即可.
解答 解:由f(x)-log2[(a-4)x+2a-5]=0,
得log2($\frac{1}{x}$+a)-log2[(a-4)x+2a-5]=0,
即log2($\frac{1}{x}$+a)=log2[(a-4)x+2a-5],
即$\frac{1}{x}$+a=(a-4)x+2a-5>0,①
则(a-4)x2+(a-5)x-1=0,
即(x+1)[(a-4)x-1]=0,②,
当a=4时,方程②的解为x=-1,代入①,成立;
当a=3时,方程②的解为x=-1,代入①,成立;
当a≠4且a≠3时,方程②的解为x=-1或x=$\frac{1}{a-4}$,
若x=-1是方程①的解,则$\frac{1}{x}$+a=a-1>0,即a>1,
若x=$\frac{1}{a-4}$是方程①的解,则$\frac{1}{x}$+a=2a-4>0,即a>2,
则要使方程①有且仅有一个解,则1<a≤2.
综上,若方程f(x)-log2[(a-4)x+2a-5]=0的解集中恰好有一个元素,则a的取值范围是1<a≤2,或a=3或a=4.
点评 本题考查对数的运算性质,考查数学转化思想方法和分类讨论的数学思想方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (3,$\frac{π}{2}$) | C. | (-3,$\frac{2π}{3}$) | D. | (3,$\frac{11π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=2 | B. | k=2$\sqrt{2}$ | C. | k=$\sqrt{2}$ | D. | k=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥V-ABC中,VA=VB=VC=2$\sqrt{3}$,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF分别交VB,VC于点E,F,求△AEF周长的最小值.
如图,在三棱锥V-ABC中,VA=VB=VC=2$\sqrt{3}$,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF分别交VB,VC于点E,F,求△AEF周长的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
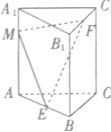 如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )
如图,已知ABC-A1B1C1是所有棱长均相等的正三棱柱,点E是棱AB的中点,点F是棱B1C1的中点,点M是棱AA1上的动点,则二面角B1-EM-F的正切值不可能等于( )| A. | $\frac{\sqrt{15}}{6}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{5}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com