
| sinx |
| x |
| ҰР |
| 2 |
| ҰР |
| 2 |
| ҰР |
| 2 |
| ҰР |
| 3 |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| x8 |
| 9! |
| x10 |
| 11! |
| ҰР |
| 2 |
| 2 |
| ҰР |
| sinx |
| x |
| ҰР |
| 2 |
| ҰР |
| 2 |
| sinx |
| x |
| ҰР |
| 2 |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| x8 |
| 9! |
| x10 |
| 11! |
| ҰР |
| 2 |
| sinx |
| x |
| cosx•x-sinx |
| x2 |
| x-tanx |
| x2 |
| ҰР |
| 2 |
| ҰР |
| 2 |
| ҰР |
| 2 |
| ҰР |
| 2 |
| sinx |
| x |
| ҰР |
| 2 |
| 2 |
| ҰР |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| x8 |
| 9! |
| x10 |
| 11! |
| ҰР |
| 3 |
| ҰР |
| 2 |
| 2 |
| ҰР |
| 2 |
| ҰР |


 ЦЗ»ЫРЎёҙП°ПөБРҙр°ё
ЦЗ»ЫРЎёҙП°ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
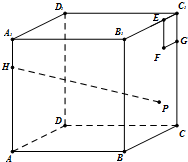 ИзНјЈ¬ТСЦӘХэ·ҪМеABCD-A1B1C1D1АвіӨОӘ4Ј¬өгHФЪАвAA1ЙПЈ¬ЗТHA1=1Ј®ФЪІаГжBCC1B1ДЪЧчұЯіӨОӘ1өДХэ·ҪРОEFGC1Ј¬PКЗІаГжBCC1B1ДЪТ»¶ҜөгЈ¬ЗТөгPөҪЖҪГжCDD1C1ҫаАлөИУЪПЯ¶ОPFөДіӨЈ®ФтөұөгPФЛ¶ҜКұЈ¬|HP|2өДЧоРЎЦөКЗЈЁЎЎЎЎЈ©
ИзНјЈ¬ТСЦӘХэ·ҪМеABCD-A1B1C1D1АвіӨОӘ4Ј¬өгHФЪАвAA1ЙПЈ¬ЗТHA1=1Ј®ФЪІаГжBCC1B1ДЪЧчұЯіӨОӘ1өДХэ·ҪРОEFGC1Ј¬PКЗІаГжBCC1B1ДЪТ»¶ҜөгЈ¬ЗТөгPөҪЖҪГжCDD1C1ҫаАлөИУЪПЯ¶ОPFөДіӨЈ®ФтөұөгPФЛ¶ҜКұЈ¬|HP|2өДЧоРЎЦөКЗЈЁЎЎЎЎЈ©| AЎў21 | BЎў22 | CЎў23 | DЎў25 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| x2 |
| 4 |
| y2 |
| 3 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| y2 |
| 2 |
| PA1 |
| PF2 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| a |
| b |
| a |
| b |
2
| ||
| 3 |
| 5ҰР |
| 12 |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com