数列0.7.0.77.0.777.-.0.$\underset{\underbrace{77-7}}{n个}$.-的前10项和为$\frac{70}{9}$-$\frac{7}{81}(1-\frac{1}{1{0}^{10}})$．题目和参考答案——青夏教育精英家教网—

2．数列0.7，0.77，0.777，…，0.$\underset{\underbrace{77…7}}{n个}$，…的前10项和为$\frac{70}{9}$-$\frac{7}{81}（1-\frac{1}{1{0}^{10}}）$．

分析由0.$\underset{\underbrace{77…7}}{n个}$=$\frac{7}{9}$×（10ⁿ-1）×10^-n=$\frac{7}{9}×（1-\frac{1}{1{0}^{n}}）$．利用等比数列的前n项和公式即可得出．

解答解：∵0.$\underset{\underbrace{77…7}}{n个}$=$\frac{7}{9}$×（10ⁿ-1）×10^-n=$\frac{7}{9}×（1-\frac{1}{1{0}^{n}}）$．
∴数列0.7，0.77，0.777，…，0.$\underset{\underbrace{77…7}}{n个}$，…的前10项和S₁₀=$\frac{7×10}{9}$-$\frac{7}{9}×\frac{\frac{1}{10}×（1-\frac{1}{1{0}^{10}}）}{1-\frac{1}{10}}$
=$\frac{70}{9}$-$\frac{7}{81}（1-\frac{1}{1{0}^{10}}）$．
故答案为：$\frac{70}{9}$-$\frac{7}{81}（1-\frac{1}{1{0}^{10}}）$．

点评本题考查了等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

12．

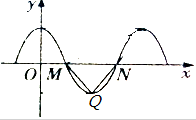函数f（x）=Acosωx（A＞0，ω＞0）部分图象如图所示，其中M，N（12，0），Q分别是函数图象在y轴右侧第一，二个零点，第一个最低点，且△MQN是等边三角形．求函数f（x）的解析式．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．已知向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（2-3x，2），$\overrightarrow{c}$=（-1，2），若$\overrightarrow{a}$⊥（$\overrightarrow{b}+\overrightarrow{c}$），则x的值为（　　）

A．

-1

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．已知α为第三象限角，且f（α）=$\frac{sin（\frac{3π}{2}-a）cos（\frac{π}{2}-a）+tan（-a+π）}{sin（\frac{π}{2}+a）tan（2π-a）}$．
（1）化简f（α）；
（2）若α=-$\frac{32}{3}$π，求f（α）的值．
（3）若f（α）=-$\frac{26}{5}$，求cos（π+α）的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．求z=600x+300y的最大值，使式中的x，y满足约束条件$\left\{\begin{array}{l}{3x+y≤300}\\{x+2y≤252}\\{x≥0}\\{y≥0}\end{array}\right.$的整数解．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．已知数列{a_n}，{b_n}都是等差数列，S_n，T_n分别是它们的前n项和，并且$\frac{S_n}{T_n}=\frac{7n+3}{n+3}$，则$\frac{{{a_2}+{a_5}+{a_{19}}+{a_{24}}}}{{{b_8}+{b_{10}}+{b_{14}}+{b_{18}}}}$=$\frac{19}{3}$．（用最简分数作答）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．已知复数z满足|z+4-3i|=2（i为虚数单位）．则|z|的最大值为7．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．“θ≠$\frac{π}{3}$”是“tanθ≠$\sqrt{3}$”的（　　）