
分析 (1)运用a0=1,令x-2=0,则x=2,求得g(2)=2,代入f(x),即可求得a=1;
(2)运用对数函数的单调性,当a>1时,f(x)在x>0上递增,解不等式即可得到;
(3)求出h(x),分别画出y=h(x)与y=2b的图象,由图象可知:0<2b<1,即可求出b的范围.
解答 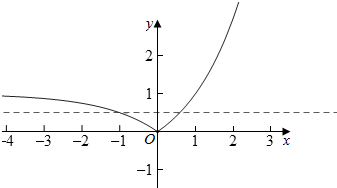 解:(1)函数g(x)的图象恒过定点A,当x-2=0时,即x=2,y=2,
解:(1)函数g(x)的图象恒过定点A,当x-2=0时,即x=2,y=2,
∴A点的坐标为(2,2),
又A点在f(x)上,
∴f(2)=$lo{g}_{\sqrt{3}}(2+a)$=a,解得a=1,
(2)f(x)<${log_{\sqrt{3}}}a$,
∴$lo{g}_{\sqrt{3}}(x+1)$<$lo{g}_{\sqrt{3}}1$=0,
∴0<x+1<1,
∴-1<x<0,
∴不等式的解集为(-1,0),
(3)由(1)知g(x)=g(x)=2x-2+1,
∴h(x)=|g(x+2)-2|=|2x-1|=2b,
分别画出y=h(x)与y=2b的图象,如图所示:
由图象可知:0<2b<1,故b的取值范围为$({0,\frac{1}{2}})$
点评 本题考查指数函数的图象的特点,考查对数函数的单调性的运用:解不等式,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
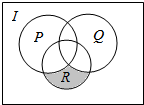 已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )
已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )| A. | R∩∁I(P∪Q) | B. | R∩∁I(P∩Q) | C. | (R∩∁IP)∩Q | D. | (R∩∁IQ)∩P |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com