
分析 由a1=1,且对任意的m,n∈N*都有:am+n=am+an+mn,令m=1可得:an+1=an+a1+n,即an+1-an=1+n,利用“累加求和”即可得到an,再利用“裂项求和”即可得出.
解答 解:由a1=1,且对任意的m,n∈N*都有:am+n=am+an+mn,
令m=1可得:an+1=an+a1+n,∴an+1-an=1+n,
∴an=a1+(a2-a1)+…+(an-an-1)
=1+2+…+n=$\frac{1}{2}$n(n+1),
∴an=$\frac{1}{2}$n(n+1),
∴$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴$\frac{1}{a_1}$+$\frac{1}{a_2}$+$\frac{1}{a_3}$+…+$\frac{1}{a_{2012}}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$)=2(1-$\frac{1}{2013}$)=$\frac{4024}{2013}$,
故答案为:$\frac{4024}{2013}$
点评 本题考查数列的前2013项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤1 | C. | a≤-$\frac{\sqrt{2}}{2}$ | D. | a$≤\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
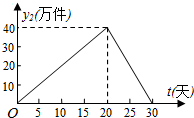 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(万件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x<0 | B. | ?x∈R,2x<0 | C. | ?x0∈R,2${\;}^{{x}_{0}}$≤0 | D. | ?3x0∈R,2${\;}^{{x}_{0}}$<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com