练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
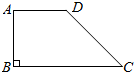
    7．如图所示，已知AB是直角梯形ABCD与底边垂直的一腰，分别以AB，CD，DA为轴旋转，试说明所得几何体的结构特征．

    分析 根据旋转体的结构特征，得出：
    ①以AB所在直线为轴旋转一周，所得几何体是圆台；
    ②以CD所在直线为轴旋转一周时，所得几何体是简单组合体；
    ③以DA所在直线为轴旋转一周时，所得几何体是简单组合体．

    解答 解：由题意知，①将此梯形以AB所在直线为轴旋转一周，所得几何体是圆台，
    且圆台上底圆的半径是AD，下底圆的半径是BC，高是AB，母线长是CD；
    ②将此梯形以CD所在直线为轴旋转一周时，所得几何体的上部是圆台挖去个圆锥，
    下部是圆锥的组合体，如图所示；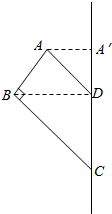

    ③将此梯形以DA所在直线为轴旋转一周，所得几何体是圆柱挖去一个圆锥体的组合体，如图所示；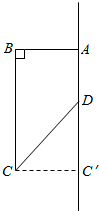

    点评 本题考查了旋转体的结构特征的应用问题，解题的关键是由平面图形想象出所得旋转体的结构特征，也考查了空间想象能力的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．使得指数函数y=（3a-2a2）x为增函数的实数a的集合为A，不等式x2-2x+1-m2≤0（m＞0）的解集为B．
    （1）求集合A、B；
    （2）若“x∈A”是“x∈B”的充分不必要条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合A={y|y=2x，x∈R}，B={y|y=x2，x∈R}，则（　　）
    A．A∪B=AB．A∩B=AC．A=BD．A∩B=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A又在函数$f（x）={log_{\sqrt{3}}}（x+a）$的图象上．
    （1）求实数a的值；                
    （2）解不等式f（x）＜${log_{\sqrt{3}}}a$；
    （3）函数h（x）=|g（x+2）-2|的图象与直线y=2b有两个不同的交点时，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，在直角坐标系中，画出过点（0，1）且与已知直线l垂直的直线l′，并求出直线l′的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．不等式sinx＞a在x∈（-$\frac{π}{4}$，$\frac{π}{2}$）上恒成立，则a的取值范围为（　　）
    A．a＞1B．a≤1C．a≤-$\frac{\sqrt{2}}{2}$D．a$≤\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知-$\frac{π}{2}$＜x＜0，sinx+cosx=$\frac{1}{5}$．
    （1）求sin2x和cosx-sinx；
    （2）求$\frac{sin2x+2si{n}^{2}x}{1-tanx}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列函数中是奇函数的为（　　）
    A．y=$\frac{{x}^{2}+cosx}{{x}^{2}-cosx}$B．y=$\frac{sinx+cosx}{sinx-cosx}$
    C．y=2cosxD．y=lg（sinx+$\sqrt{1+si{n}^{2}x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．教师想从52个学生中，利用简单随机抽样的方法，抽取10名谈谈学习社会主义核心价值观的体会，一小孩在旁边随手拿了两个号签，教师没在意，在余下的50个号签中抽了10名学生，则其中的李明同学的签被小孩拿去和被教师抽到的概率分别为（　　）
    A．$\frac{1}{26}，\frac{1}{5}$B．$\frac{1}{26}$，$\frac{5}{26}$C．$\frac{1}{26}$，0D．$\frac{1}{25}$，$\frac{1}{5}$

    查看答案和解析>>

    同步练习册答案