
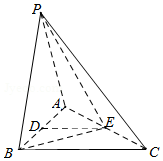
 如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$
如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$分析 (Ⅰ)证明:DE∥BC,即可证明DE∥平面PBC;
(Ⅱ)证明:AB⊥平面PDE,即可证明AB⊥PE;
(Ⅲ)利用等体积方法,求点D到平面PBE的距离.
解答 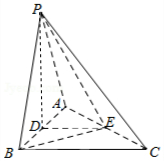 (Ⅰ)证明:∵D、E分别为AB、AC边中点,
(Ⅰ)证明:∵D、E分别为AB、AC边中点,
∴DE∥BC,
∵DE?平面PBC,BC?平面PBC,
∴DE∥平面PBC;
(Ⅱ)证明:连接PD,则
∵AB⊥BC,DE∥BC,
∴AB⊥DE,
∵等边三角形PAB,D为AB的中点,
∴PD⊥AB,
∵PD∩DE=D,
∴AB⊥平面PDE,
∵PE?平面PDE,
∴AB⊥PE;
(Ⅲ)解:∵平面PAB⊥平面ABC,PD⊥AB,
∴PD⊥平面ABC,
∵D为AB中点,AB=2,
∴PD=$\sqrt{3}$,
∴VP-ABC=$\frac{1}{3}•\frac{1}{2}•AB•BC•PD$=2,
∵E是AC的中点,
∴S△ABE=$\frac{1}{2}{S}_{△BAC}$,
∴S△BDE=$\frac{1}{4}{S}_{△ABC}$,
∴VP-BCE=$\frac{1}{4}$VP-ABC=$\frac{1}{2}$,
∵BE=$\frac{1}{2}AC$=2,∴PE=$\sqrt{P{D}^{2}+D{E}^{2}}$=$\sqrt{6}$,
∵B到PE的距离为$\sqrt{B{P}^{2}-\frac{1}{4}P{E}^{2}}$=$\frac{\sqrt{10}}{2}$,
∴S△BPE=$\frac{1}{2}×\sqrt{6}×\frac{\sqrt{10}}{2}$=$\frac{\sqrt{15}}{2}$,
设点D到平面PBE的距离为h,则$\frac{1}{3}×\frac{\sqrt{15}}{2}h$=$\frac{1}{2}$,∴h=$\frac{\sqrt{15}}{5}$.
点评 本题主要考查空间直线与平面的位置关系,考查线面平行和垂直的判定和性质,熟记定理是解题的关键,同时注意解题的规范.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{2^{n-1}}}}$ | B. | $\frac{1}{{{2^n}-1}}$ | C. | $\frac{1}{{{3^{n-1}}}}$ | D. | $\frac{1}{{{2^{n-1}}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 108 | B. | 120 | C. | 72 | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 504 | B. | 1008 | C. | 1009 | D. | 2017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com