
分析 根据题意,由抛物线的方程可得其焦点坐标以及准线方程,设所求点坐标为P(x,y),作PQ⊥l于Q,由抛物线的定义分析可得P到准线的距离等于P、Q的距离,即x+1=3,解可得x的值,将x的值代入抛物线方程即可得y的值,综合即可得答案.
解答  解:∵抛物线方程为y2=4x,∴焦点为F(1,0),
解:∵抛物线方程为y2=4x,∴焦点为F(1,0),
准线为l:x=-1.
设所求点坐标为P(x,y),作PQ⊥l于Q.
根据抛物线定义可知P到准线的距离等于P、Q的距离,
即x+1=3,
解之得x=2,代入抛物线方程求得y=±2$\sqrt{2}$,
∴点P坐标为:(2,±2$\sqrt{2}$).
故答案为:(2,±2$\sqrt{2}$).
点评 本题考查抛物线的几何性质,关键是利用抛物线的几何性质进行转化.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
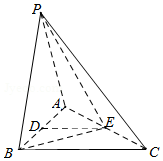 如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$
如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 55.2,3.6 | B. | 55.2,56.4 | C. | 64.8,63.6 | D. | 64.8,3.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com