
分析 (Ⅰ)根据sinA、sinB、sinC成等差数列,以及三角形的内角和即可求出sin$\frac{B}{2}$,再利用倍角公式即可求出,
(Ⅱ)根据余弦定理得到a,b,c的关系,再由正弦定理可得a,c的关系,即可求出ac,再根据三角形的面积公式计算即可.
解答 解:(Ⅰ)∵A、B、C为△ABC的内角,且$C-A=\frac{π}{3}$.
∴由A+B+C=π,可得$\left\{\begin{array}{l}A=\frac{π}{3}-\frac{B}{2}\\ C=\frac{2π}{3}-\frac{B}{2}\end{array}\right.$(*),
∵sinA、sinB、sinC的值成等差数列,
∴sinA+sinC=2sinB
将(*)代入上式,化简得$sin\frac{B}{2}=\frac{{\sqrt{3}}}{4}$.
∴$cosB=1-2{sin^2}\frac{B}{2}$=$\frac{5}{8}$.
(Ⅱ)∵$b=\sqrt{13}$,$cosB=\frac{5}{8}$
由余弦定理,得b2=13=a2+c2$-\frac{5}{4}ac={({a+c})^2}$$-\frac{13}{4}ac$
又∵sinA、sinB、sinC的值成等差数列,
由正弦定理,得$a+c=2b=2\sqrt{13}$,
∴$13=52-\frac{13}{4}ac$,解得ac=12.
由$cosB=\frac{5}{8}$,得$sinB=\frac{{\sqrt{39}}}{8}$,
∴△ABC的面积${S_{△ABC}}=\frac{1}{2}acsinB$=$\frac{1}{2}×12×\frac{{\sqrt{39}}}{8}=\frac{{3\sqrt{39}}}{4}$
点评 此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 6x-y+6=0 | B. | x-3y+1=0 | C. | 6x+y+6=0 | D. | x+3y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
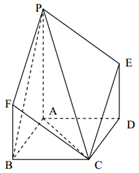 如图,点P是菱形ABCD所在平面外一点,PA⊥平面ABCD,PA∥FB∥ED,∠ABC=60°,PA=AB=2BF=2DE.
如图,点P是菱形ABCD所在平面外一点,PA⊥平面ABCD,PA∥FB∥ED,∠ABC=60°,PA=AB=2BF=2DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{2^{n-1}}}}$ | B. | $\frac{1}{{{2^n}-1}}$ | C. | $\frac{1}{{{3^{n-1}}}}$ | D. | $\frac{1}{{{2^{n-1}}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com