
分析 由题意知两人取球包含的基本事件总数n=16,其中满足两人为“好朋友”的共有4种情况,由此能求出甲、乙两人成为“好朋友”的概率.
解答 解:由题意知两人取球包含的基本事件总数n=16,分别为:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),
其中满足两人为“好朋友”的共有4种情况,分别为:(1,1),(2,2),(3,3),(4,4),
∴甲、乙两人成为“好朋友”的概率为p=$\frac{4}{16}=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查概率的求法,考查古典概型等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
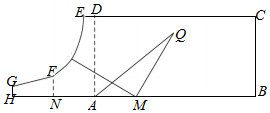 如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).
如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com