
分析 (1)由题意得:$\left\{\begin{array}{l}{c=a-c}\\{\frac{1}{2}(a-c)=\frac{\sqrt{3}}{2}}\\{{a}^{2}={c}^{2}+{b}^{2}}\end{array}\right.$,解得a;
(2)设M(x1,y1),N(x2,y2),直线l 的方程为y=kx+2,将y=kx+2 代入椭圆方程得(3+4k2)x2+16kx+4=0,${x_1}+{x_2}=\frac{-16k}{{3+4{k^2}}},{x_1}{x_2}=\frac{4}{{3+4{k^2}}}$,直线NQ 的方程$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}+{x_1}}}(x+{x_1})$,由对称性可知,若过定点,则必在y 轴上,令x=0,即可.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{c=a-c}\\{\frac{1}{2}(a-c)=\frac{\sqrt{3}}{2}}\\{{a}^{2}={c}^{2}+{b}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\end{array}\right.$,
∴a的值为2;
(2)设M(x1,y1),N(x2,y2),直线l 的方程为y=kx+2,
则Q(-x1,y1),
将y=kx+2 代入椭圆方程得(3+4k2)x2+16kx+4=0,
${x_1}+{x_2}=\frac{-16k}{{3+4{k^2}}},{x_1}{x_2}=\frac{4}{{3+4{k^2}}}$,
直线NQ 的方程$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}+{x_1}}}(x+{x_1})$,
由对称性可知,若过定点,则必在y 轴上,
令x=0,得$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}+{x_1}}}{x_1}$,$y=\frac{{{x_2}{y_1}+{x_1}{y_2}}}{{{x_1}+{x_2}}}=\frac{{2k{x_1}{x_2}}}{{{x_1}+{x_2}}}+2=\frac{3}{2}$,
所以直线NQ 经过定点(0,$\frac{3}{2}$).
点评 本题考查了椭圆的方程,直线与椭圆的位置关系,直线过定点问题,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\sqrt{3}}]$ | B. | $[{-2,\sqrt{3}}]$ | C. | $[{-\sqrt{3},2}]$ | D. | $[{1,\sqrt{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
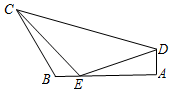 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于原点对称 | B. | 关于直线 y=-x 对称 | ||
| C. | 关于y轴对称 | D. | 关于直线y=x 对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com