
分析 (1)求出函数的导数,解关于导函数的方程,求出函数的单调区间,得到函数的极值即可;
(2)求出函数h(x)的导数,通过讨论a的范围,求出函数的单调区间,得到函数的极值点,求出m的范围即可.
解答 解:(1)f(x)的定义域是(0,+∞),
令f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$=0,解得:x=1,
x∈(0,1)时,f′(x)<0,f(x)递减,
x∈(1,+∞)时,f(x)递增,
∴f(x)在x=1处取得极小值,且极小值f(1)=2,无极大值,
令g′(x)=1-$\frac{1}{{x}^{2}}$=0,解得:x=1(x=-1舍去),
∴当x∈(0,1)时,g′(x)<0,g(x)递减,
当x∈(1,+∞)时,g′(x)>0,g(x)递增,
∴g(x)在x=1处取得极小值,且极小值g(1)=2,无极大值,
故两个函数有相同的极小值点x=1,且所求的极小值是2;
(2)h(x)=f(x)-ag(x)=lnx+$\frac{1}{x}$+1-ax-$\frac{a}{x}$,其定义域是(0,+∞),
则h′(x)=$\frac{-(x-1)(ax+a-1)}{{x}^{2}}$,
a=0时,h′(x)=0仅有1个解,x=1不合题意,
当a≠0时,令h′(x)=0,解得:x=1或x=$\frac{1-a}{a}$,
由题意得:$\frac{1-a}{a}$>0,且$\frac{1-a}{a}$≠1,∴a∈(0,$\frac{1}{2}$)∪($\frac{1}{2}$,1),
此时,h(x)的两个极值点分别是x=1和x=$\frac{1-a}{a}$,
当a∈(0,$\frac{1}{2}$)时,$\frac{1-a}{a}$>1,∴x1=1,x2=$\frac{1-a}{a}$,h(x1)=h(1)=2-2a,
而当2-2a∈(1,2),又h(x1)<m恒成立,则m≥2,
当a∈($\frac{1}{2}$,1)时,$\frac{1-a}{a}$<1,∴x1=$\frac{1-a}{a}$,x2=1,
h(x1)=h($\frac{1-a}{a}$)=ln$\frac{1-a}{a}$+2a,
设ω(a)=ln$\frac{1-a}{a}$+2a,则ω′(a)=-$\frac{{2(a-\frac{1}{2})}^{2}+\frac{1}{2}}{a(1-a)}$<0,
∴ω(a)在($\frac{1}{2}$,1)上是减函数,ω(a)<ω($\frac{1}{2}$)=1,
∴h(x1)=ln$\frac{1-a}{a}$+2a<1,
又h(x1)<m恒成立,则m≥1,
综上,实数m的范围是[2,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
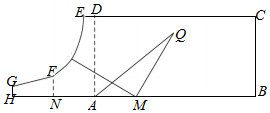 如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).
如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{12}$h | B. | $\frac{3}{4}$h | C. | $\frac{1}{2}$h | D. | h |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图多面体ABCD中,面ABCD为正方形,棱长AB=2,AE=3,DE=$\sqrt{5}$,二面角E-AD-C的余弦值为$\frac{{\sqrt{5}}}{5}$,且EF∥BD.
如图多面体ABCD中,面ABCD为正方形,棱长AB=2,AE=3,DE=$\sqrt{5}$,二面角E-AD-C的余弦值为$\frac{{\sqrt{5}}}{5}$,且EF∥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com