
 已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.分析 由已知球的表面积求出球的半径,再由棱锥的高可得球心到正四棱锥底面中心的距离,求解三角形得正四棱锥的底面边长.
(1)找出异面直线BP和AD所成角,求解三角形可得异面直线BP和AD所成角的余弦值;
(2)利用等积法求点E到平面PAD的距离.
解答 解:由球的表面积公式S=4πR2,得球的半径$R=\frac{13}{6}$,
设球心为O1,在正四棱锥P-ABCD中,高为PO,则O1必在PO上,
连AO1,则${O_1}O=\frac{5}{6},A{O_1}=\frac{13}{6}$,
则在Rt△O1OA,有$OO_1^2+O{A^2}={O_1}{A^2}$,
即OA=2,可得正方形ABCD的边长为$2\sqrt{2}$,
侧棱$PA=\sqrt{O{P^2}+O{A^2}}=\sqrt{13}$.
(1)在正方形ABCD中,BC∥AD,∠PBC是异面直线BP和AD所成的角或其补角,
取BC中点M,在等腰△PBC中,可得PM⊥BC,斜高$PM=\sqrt{11}$,
则在Rt△PMB中,$cos∠PBC=\frac{BM}{PB}=\frac{{\sqrt{2}}}{{\sqrt{13}}}=\frac{{\sqrt{26}}}{13}$,
∴异面直线BP和AD所成的角的余弦值为$\frac{{\sqrt{26}}}{13}$;
(2)由O,E为CA,CP中点,得OE∥AP,
且满足OE?平面PAD,AP?平面PAD,∴OE∥平面PAD,
∴E到平面PAD的距离等于O到平面PAD的距离,
又∵${S_{△PAD}}=\frac{1}{2}•2\sqrt{2}•\sqrt{11}=\sqrt{22},{S_{△AOD}}=\frac{1}{2}•2•2=2$,
再设O到平面PAD的距离为h,则由VE-PAD=VO-PAD=VP-AOD,
可得$\frac{1}{3}•{S_{△PAD}}•h=\frac{1}{3}•{S_{△AOD}}•PO$,则$h=\frac{{3\sqrt{22}}}{11}$,
∴点E到平面PAD的距离$\frac{{3\sqrt{22}}}{11}$.
点评 本题考查空间中点线面间的距离计算,考查异面直线所成角的求法,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
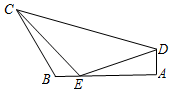 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| B. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m”为真命题 | |
| C. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| D. | 若命题P:?n∈N,2n>1000,则?P:?n∈N,2n>1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com