练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．有100件产品编号从00到99，用系统抽样方法从中抽取5件产品进行检验，分组后每组按照相同的间隔抽取产品，若第5组抽取的产品编号为91，则第2组抽取的产品编号为31．

    分析 根据系统抽样原理的抽样间隔相等，求出第1组抽取的数据，再求第2组抽取的产品编号．

    解答 解：根据系统抽样原理，抽样间隔为l=$\frac{100}{5}$=20，
    设第一组抽取数据为a0，
    则第5组抽取的产品编号为4×20+a0=91，
    解得a0=11；
    所以第2组抽取的产品编号为1×20+a0=31．
    故答案为：31．

    点评 本题考查了系统抽样原理应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知集合M={0，1}，集合N满足M∪N={0，1}，则集合N共有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定积分${∫}_{1}^{e}$$\frac{1}{x}$dx的值等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知F1（-1，0），F2（1，0），曲线C1上任意一点M满足$|{M{F_2}}|-|{M{F_1}}|=\sqrt{2}$；曲线C2上的点N在y轴的右边且N到F2的距离与它到y轴的距离的差为1．
    （1）求C1，C2的方程；
    （2）过F1的直线l与C1相交于点A，B，直线AF2，BF2分别与C2相交于点C，D和E，F．求$\sqrt{|{CD}|•|{EF}|}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设集合$A=\left\{{-1\;，0\;，\frac{1}{2}\;，3}\right\}$，B={x|x≥1}，则A∩B={3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设x＞0，y＞0，z＞0，xyz=1，求证：$\frac{1}{{x}^{3}y}$+$\frac{1}{{y}^{3}z}$+$\frac{1}{{z}^{3}x}$≥$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

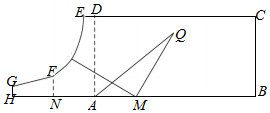    7．如图，某地区有一块长方形植物园ABCD，AB=8（百米），BC=4（百米），植物园西侧有一块荒地，现计划利用该荒地扩大植物园面积，使得新的植物园为HBCEFG满足下列要求：E在CD的延长线上，H在BA的延长线上，DE=0.5（百米），AH=4（百米），N为AH的中点，FN⊥AH，EF为曲线段，它上面的任意一点到AD与AH的距离乘积为定值，FG，GH均为线段，GH⊥HA，GH=0.5（百米）．
    （1）求四边形FGHN的面积；
    （2）已知音乐广场M在AB上，AM=2（百米），若计划在EFG的某一处P开一个植物园大门，在原植物园ABCD内选一点Q，为中心建一个休息区，使得QM=PM，且∠QMP=90°，问点P在何处，AQ最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知球内接正四棱锥P-ABCD的高为3，AC，BC相交于O，球的表面积为$\frac{169π}{9}$，若E为PC中点．
    （1）求异面直线BP和AD所成角的余弦值；
    （2）求点E到平面PAD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知等比数列{an}的前n项和为Sn，若S6=$\frac{21}{2}$，公比q=-$\frac{1}{2}$．
    （1）求数列{an}的通项公式；
    （2）求和：a12+a22+a32+…+an2．

    查看答案和解析>>

    同步练习册答案