
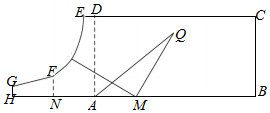
 如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).
如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).分析 (1)建立坐标系,根据E点坐标得出曲线EF的方程,从而得出F点坐标,代入梯形的面积公式即可;
(2)设P(x,y),用x,y表示出$\overrightarrow{MQ}$,$\overrightarrow{AQ}$,根据Q点位置求出x的范围得出P在曲线EF上,利用距离公式和基本不等式的性质得出AQ最小时的x的值即可得出P点位置.
解答  解:(1)以A为原点,以AB,AD所在直线为坐标轴建立平面直角坐标系xOy,如图所示:
解:(1)以A为原点,以AB,AD所在直线为坐标轴建立平面直角坐标系xOy,如图所示:
则E(-$\frac{1}{2}$,4),∴曲线EF的方程为y=-$\frac{2}{x}$,
∴F(-2,1),N(-2,0),H(-4,0),G(-4,$\frac{1}{2}$),
∴FN=1,GH=$\frac{1}{2}$,HN=2,
∴四边形FGHN的面积为S=$\frac{1}{2}×(\frac{1}{2}+1)×2$=$\frac{3}{2}$(平方百米).
(2)设P(x,y),则$\overrightarrow{MP}$=(x-2,y),$\overrightarrow{MQ}$=(y,2-x),$\overrightarrow{AQ}$=(2+y,2-x),
∴$\left\{\begin{array}{l}{0≤2+y≤8}\\{0≤2-x≤4}\end{array}\right.$,解得-2≤x≤2,
∴P点在曲线EF上,-2≤x≤-$\frac{1}{2}$,∴y=-$\frac{2}{x}$,
∴|AQ|=$\sqrt{(2+y)^{2}+(2-x)^{2}}$=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}-4x-\frac{8}{x}+8}$=$\sqrt{(x+\frac{2}{x})^{2}-4(x+\frac{2}{x})+4}$=$\sqrt{(x+\frac{2}{x}-2)^{2}}$=-x-$\frac{2}{x}$+2≥2$\sqrt{2}$+2,
当且仅当-x=$\frac{2}{-x}$即x=-$\sqrt{2}$时取等号.
∴当P为(-$\sqrt{2}$,-$\sqrt{2}$)时,|AQ|最小.
点评 本题考查了平面向量的应用,不等式的性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}或3$ | B. | $-\frac{1}{2}或3$ | C. | $\frac{1}{2}或1$ | D. | $-\frac{1}{2}或1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com