
分析 (1)判断点M的轨迹是以F1,F2为焦点,$\sqrt{2}$为实轴长的双曲线的左支,然后求解椭圆方程.设N(x,y)(x>0),则有$\sqrt{{{({x-1})}^2}+{y^2}}-x=1$,化简可得C2的方程.
(2)设直线l的方程为x=ky-1(0≤k2<1),联立方程组$\left\{{\begin{array}{l}{x=ky-1}\\{{x^2}-{y^2}=\frac{1}{2}}\end{array}}\right.$,消去x,设A(x1,y1),B(x2,y2),利用韦达定理转化求解斜率关系,直线AF2的方程为y=k1(x-1),代入y2=4x,求出CD,EF然后推出结果.
解答 解:(1)由题意可知点M的轨迹是以F1,F2为焦点,$\sqrt{2}$为实轴长的双曲线的左支,故有$a=\frac{{\sqrt{2}}}{2},c=1⇒b=\frac{{\sqrt{2}}}{2}$,
∴C1的方程为${x^2}-{y^2}=\frac{1}{2}({x<0})$,
设N(x,y)(x>0),则有$\sqrt{{{({x-1})}^2}+{y^2}}-x=1$,化简得y2=4x(x>0),
即C2的方程为y2=4x(x>0).
(2)设直线l的方程为x=ky-1(0≤k2<1),
联立方程组$\left\{{\begin{array}{l}{x=ky-1}\\{{x^2}-{y^2}=\frac{1}{2}}\end{array}}\right.$,消去x得$({{k^2}-1}){y^2}-2ky+\frac{1}{2}=0$,
设A(x1,y1),B(x2,y2),则有$\left\{{\begin{array}{l}{{y_1}+{y_2}=\frac{2k}{{{k^2}-1}}}\\{{y_1}{y_2}=\frac{1}{{2({{k^2}-1})}}}\end{array}}\right.$,
设AF2,BF2的斜率分别为k1,k2,则有$\left\{{\begin{array}{l}{{k_1}=\frac{y_1}{{{x_1}-1}}=\frac{y_1}{{k{y_1}-2}}}\\{{k_2}=\frac{y_2}{{{x_2}-1}}=\frac{y_2}{{k{y_2}-2}}}\end{array}}\right.$,
∴$\frac{1}{k_1}+\frac{1}{k_2}=({k-\frac{2}{y_1}})+({k-\frac{2}{y_2}})=2k-2({\frac{1}{y_1}+\frac{1}{y_2}})=-6k$,$\frac{1}{k_1}•\frac{1}{k_2}={k^2}-2k({\frac{1}{y_1}+\frac{1}{y_2}})+\frac{4}{{{y_1}{y_2}}}={k^2}-8$,
直线AF2的方程为y=k1(x-1),代入y2=4x有$k_1^2{x^2}-({2k_1^2+4})x+k_1^2=0$,
设C(x3,y3),D(x4,y4),则有${x_3}+{x_4}=2+\frac{4}{k_1^2}$,
∴$|{CD}|=|{C{F_2}}|+|{D{F_2}}|=({{x_2}+1})+({{x_2}+1})={x_1}+{x_2}+2=4+\frac{4}{k_1^2}=4({1+\frac{1}{k_1^2}})$,
同理$|{EF}|=4({1+\frac{1}{k_2^2}})$.
∴$|{CD}||{EF}|=16({1+\frac{1}{k_1^2}})({1+\frac{1}{k_2^2}})=16[{{{({\frac{1}{k_1}+\frac{1}{k_2}})}^2}+{{({\frac{1}{{{k_1}{k_2}}}-1})}^2}}]=16[{36{k^2}+{{({{k^2}-9})}^2}}]=16{({{k^2}+9})^2}$,
∴$\sqrt{|{CD}||{EF}|}=4({{k^2}+9})∈[{36,40})$.
点评 本题考查椭圆与抛物线的方程的求法,直线与圆锥曲线的位置关系的应用,考查设而不求,思想的应用,是难题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
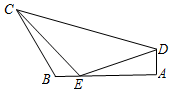 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com