
| A. | $(\frac{1}{4},\frac{13}{4})$ | B. | $(\frac{1}{4},1)$ | C. | $(1,\frac{9}{4})$ | D. | $(\frac{9}{4},\frac{13}{4})$ |
分析 求出导函数,据韦达定理求出α,β与a,b的关系,据α,β的范围求出a,b的范围,画出关于a,b的不等式组的可行域,由图数形结合
解答  解:f′(x)=x2+ax+2b,
解:f′(x)=x2+ax+2b,
∵α,β是f(x)的极值点,
所以α,β是x2+ax+2b=0的两个根,
∴α+β=-a,αβ=2b,
∵α∈(0,1),β∈(1,2),
∴1<α+β<3,0<αβ<2
∴1<-a<3,0<2b<2
令m=$\frac{a}{2}$,n=b,∴$\left\{\begin{array}{l}{-\frac{3}{2}<m<-\frac{1}{2}}\\{0<n<1}\end{array}\right.$
作出不等式组$\left\{\begin{array}{l}{-\frac{3}{2}<m<-\frac{1}{2}}\\{0<n<1}\end{array}\right.$的可行域,
则$\frac{a^2}{4}+{b^2}$表示可行域中的点(m,n)与(0,0)的距离平方m2+n2,
结合图形可得OP2=$\frac{13}{4}$,OA2=$\frac{1}{4}$,
则$\frac{a^2}{4}+{b^2}$的取值范围是($\frac{1}{4}$,$\frac{13}{4}$),
故选:A.
点评 本题考查函数在极值点处的值为0;利用线性规划求函数的最值,关键是给目标函数几何意义


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
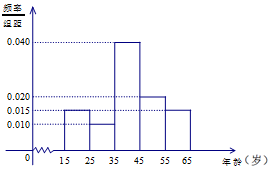 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数. | 观看方式 年龄(岁) | 电视 | 网络 |
| [15,45) | 150 | 250 |
| [45,65] | 120 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 5 | 8 | 8 | 10 | 14 | 15 | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com