
分析 由题意可得x1,x2是导函数f′(x)=x2+ax+b的两根,由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(0,1),x2∈(1,2)即$\left\{\begin{array}{l}{f′(0)=b>0}\\{f′(1)=1+a+b<0}\\{f′(2)=4+2a+b>0}\end{array}\right.$,画出满足以上条件的实数对(a,b)所构成的区域,z=(a+3)2+b2的表示点(a,b)到点(-3,0)的距离平方,即可求解
解答 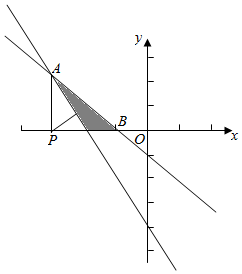 解:设f(x)的极大值点是x1,极小值点是x2,
解:设f(x)的极大值点是x1,极小值点是x2,
∵函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+bx+c在x=x1处取得极大值,在x=x2处取得极小值,
∴x1,x2是导函数f′(x)=x2+ax+b的两根,
由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(0,1),x2∈(1,2),
∴$\left\{\begin{array}{l}{f′(0)=b>0}\\{f′(1)=1+a+b<0}\\{f′(2)=4+2a+b>0}\end{array}\right.$,
则满足以上条件的实数对(a,b)所构成的区域如图所示:
由$\left\{\begin{array}{l}{1+a+b=0}\\{4+2a+b=0}\end{array}\right.$,得A(-3,2),
z=(a+3)2+b2的表示点(a,b)到点(-3,0)的距离平方,
又因为PA2=(-3--3)2+(2-0)2=4,PB2=9,
P到直线4+2a+b=0的距离等于$\frac{2}{\sqrt{5}}$,
则z=(a+3)2+b2的取值范围为($\frac{4}{5},9$),
故答案为:($\frac{4}{5}$,9).
点评 本题考查了函数的极值、根的分布及规划问题,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1.5} | B. | {x|0.5<x<2} | C. | {x|x<2} | D. | {x|1.5<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 29 | 41 | 50 | 59 | 71 |
| A. | 101.2 | B. | 108.8 | C. | 111.2 | D. | 118.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -2017 | B. | 2017 | C. | -2016 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},\frac{13}{4})$ | B. | $(\frac{1}{4},1)$ | C. | $(1,\frac{9}{4})$ | D. | $(\frac{9}{4},\frac{13}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com