
 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:分析 (Ⅰ)由频率分布直方图先求出成绩落在[70,80)上的频率,由此能补全这个频率分布直方图.
(Ⅱ)利用频率分布直方图能估计这次考试的及格率(60分及以上为及格)和平均分.
(Ⅲ)设学生甲、乙的成绩属于区间[40,50),区间[40,50)内有6名学生,现从成绩属于该区间的学生中任选两人,基本事件总数n=${C}_{6}^{2}$=15,甲、乙中至少有一人被选的对立事件是甲、乙两人没被选,由此利用对立事件概率计算公式能求出甲、乙中至少有一人被选的概率.
解答  解:(Ⅰ)由频率分布直方图得:
解:(Ⅰ)由频率分布直方图得:
成绩落在[70,80)上的频率是:1-(0.01+0.015+0.015+0.025+0.005)×10=0.3,
补全这个频率分布直方图,如图.---(3分)
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)
为1-0.01×10-0.015×10=75%
平均分:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.---(7分)
(Ⅲ)设学生甲、乙的成绩属于区间[40,50),
区间[40,50)内有:60×0.01×10=6名学生,
现从成绩属于该区间的学生中任选两人,
基本事件总数n=${C}_{6}^{2}$=15,
甲、乙中至少有一人被选的对立事件是甲、乙两人没被选,
∴甲、乙中至少有一人被选的概率p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$1-\frac{6}{15}=\frac{3}{5}$.---(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,考查频率分布直方图、概率等知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,π) | B. | $[{0,\frac{π}{4}}]∪[{\frac{3π}{4},π})$ | C. | $[{0,\frac{π}{4}}]$ | D. | $[{0,\frac{π}{4}}]∪({\frac{π}{2},π})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 阅读程序框图,并完成下列问题:
阅读程序框图,并完成下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (Ⅰ)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.设甲、乙两个班所抽取的10名同学成绩方差分别为$S_甲^2$、$S_乙^2$,比较$S_甲^2$、$S_乙^2$的大小(直接写结果,不必写过程);
(Ⅰ)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.设甲、乙两个班所抽取的10名同学成绩方差分别为$S_甲^2$、$S_乙^2$,比较$S_甲^2$、$S_乙^2$的大小(直接写结果,不必写过程);查看答案和解析>>
科目:高中数学 来源: 题型:解答题
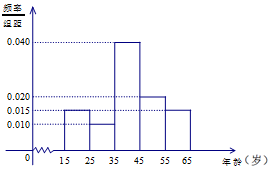 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数. | 观看方式 年龄(岁) | 电视 | 网络 |
| [15,45) | 150 | 250 |
| [45,65] | 120 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-2,3] | C. | (0,3) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com