
 在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$.
在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$. 分析 推导出sin∠ACD=$\frac{2}{\sqrt{5}}$,cos∠ACD=$\frac{\sqrt{5}}{5}$,由余弦定理得AD=$\sqrt{5}$,由正弦定理,得sinA=$\frac{4}{5}$,由此利用正弦定理能求出BC的长.
解答 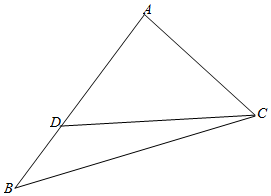 解:∵在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,
解:∵在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,
△ACD的面积为2,∠ACD为锐角,
∴S△ACD=$\frac{1}{2}×2×\sqrt{5}$×sin∠ACD=2,解得sin∠ACD=$\frac{2}{\sqrt{5}}$,
∴cos∠ACD=$\sqrt{1-(\frac{2}{\sqrt{5}})^{2}}$=$\frac{\sqrt{5}}{5}$,
∴AD=$\sqrt{5+4-2×2×\sqrt{5}×cos∠ACD}$=$\sqrt{5}$,
由正弦定理,得:$\frac{2}{sinA}=\frac{\sqrt{5}}{sin∠ACD}$,解得sinA=$\frac{2×\frac{2}{\sqrt{5}}}{\sqrt{5}}$=$\frac{4}{5}$,
又$\frac{BC}{sinA}=\frac{AC}{sinB}$,∴BC=$\frac{ACsinA}{sinB}$=$\frac{\sqrt{5}×\frac{4}{5}}{\frac{1}{2}}$=$\frac{8\sqrt{5}}{5}$.
故答案为:$\frac{8\sqrt{5}}{5}$.
点评 本题考查三角形边长的求法,涉及到正弦定理、余弦定理等基础知识,考查推理论证能力、运算求解能力,考查函数与方思想、数形结合思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
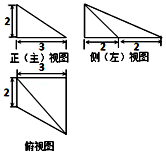
| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
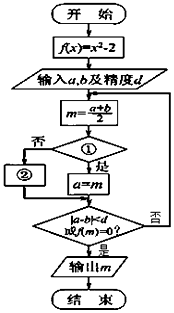
| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
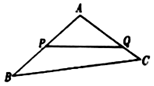 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com