
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ����ʽx1f��x1��+x2f��x2����x1f��x2��+x2f��x1���ȼ�Ϊ��x1-x2��[f��x1��-f��x2��]��0�������������ĺ���Ϊ���������������жϺ����ĵ����Լ��ɵõ����ۣ�
��� �⣺�߶�����������IJ���ʵ��x1��x2������ʽx1f��x1��+x2f��x2����x1f��x2��+x2f��x1���������
���ʽ�ȼ�Ϊ��x1-x2��[f��x1��-f��x2��]��0�������
������f��x���Ƕ�����R�ϵ���������
��y=-x2+x+1�ĶԳ�����x=$\frac{1}{2}$�������ڶ������ϲ�������������������
��y=3x-2��sinx-cosx����y��=3-2��cosx+sinx��=3-2$\sqrt{2}$sin��x+$\frac{��}{4}$����0��������������������������
��y=ex+1������������������
��f��x��=$\left\{\begin{array}{l}ln|x|{\;}_{\;}^{\;}��x��0\\ 0{\;}_{\;}^{\;}{\;}_{\;}^{\;}��x=0\end{array}$����x��0ʱ������������������x��0ʱ�����������ݼ���������������
�������㡰H�������ĺ���Ϊ�ڢۣ�
��ѡ��C��
���� ������Ҫ���麯�������Ե�Ӧ�ã�������ת��Ϊ�����ĵ����Ե���ʽ�ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ�Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �Ȳ�����ֲ���Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 60�� | C�� | 120�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
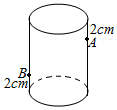 Բ���β�������8cm�������ܳ�Ϊ12cm���ڱھ౭��2cm�ĵ�A����һ�����ǣ�A�����������ڣ�����A�����ڣ��౭��2cm�ĵ�B����һС�森��С���ر����������DZ�ʳһ�٣�����Ҫ������10cm�������Ʊ��ں����С��ijߴ磩
Բ���β�������8cm�������ܳ�Ϊ12cm���ڱھ౭��2cm�ĵ�A����һ�����ǣ�A�����������ڣ�����A�����ڣ��౭��2cm�ĵ�B����һС�森��С���ر����������DZ�ʳһ�٣�����Ҫ������10cm�������Ʊ��ں����С��ijߴ磩�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com