
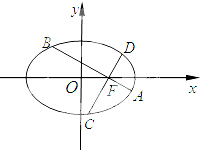
 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.分析 (1)运用椭圆的离心率公式和a,b,c的关系和弦长AB,CD,解方程可得c,进而得到椭圆方程;
(2)讨论①当两条弦中一条斜率为0时,另一条弦的斜率不存在,②当两弦斜率均存在且不为0时,设A(x1,y1),B(x2,y2),设出直线AB的方程,可得CD的方程,分别代入椭圆方程,运用韦达定理和弦长公式,再由四边形的面积公式,结合基本不等式即可得到取值范围.
解答 解:(1)由题意知,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,则a=$\frac{2\sqrt{3}}{3}$c,b=$\frac{\sqrt{3}}{3}$c,
∴AB+CD=2a+$\frac{2{b}^{2}}{a}$=$\frac{4\sqrt{3}}{3}$c+$\frac{\sqrt{3}}{3}$c=5,
所以c=$\sqrt{3}$.所以椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1.
(2)①当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意知S四边形=$\frac{1}{2}$AB•CD=$\frac{1}{2}×4×1$=2;
②当两弦斜率均存在且不为0时,设A(x1,y1),B(x2,y2),
且设直线AB的方程为y=k(x-$\sqrt{3}$),
则直线CD的方程为y=-$\frac{1}{k}$(x-$\sqrt{3}$).
将直线AB的方程代入椭圆方程中,并整理得(1+4k2)x2-8$\sqrt{3}$k2x+12k2-4=0,
所以AB=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{1+{k}^{2}}$•$\frac{4\sqrt{1+{k}^{2}}}{1+4{k}^{2}}$=$\frac{4(1+{k}^{2})}{1+4{k}^{2}}$,
同理CD=$\frac{4(1+\frac{1}{{k}^{2}})}{1+\frac{4}{{k}^{2}}}$=$\frac{4(1+{k}^{2})}{4+{k}^{2}}$.
所以S四边形=$\frac{1}{2}$AB•CD=$\frac{1}{2}$•$\frac{4(1+{k}^{2})}{1+4{k}^{2}}$•$\frac{4(1+{k}^{2})}{4+{k}^{2}}$=$\frac{8(1+{k}^{2})^{2}}{4{k}^{4}+4+17{k}^{2}}$
=$\frac{8(k+\frac{1}{k})^{2}}{4(k+\frac{1}{k})^{2}+9}$=2-$\frac{18}{4(k+\frac{1}{k})^{2}+9}$,
由4(k+$\frac{1}{k}$)2+9≥4(2$\sqrt{k•\frac{1}{k}}$)2+9=25,当且仅当k=±1时取等号.
∴S四边形∈[$\frac{32}{25}$,2),
综合①与②可知,S四边形∈[$\frac{32}{25}$,2).
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程和椭圆方程,运用韦达定理和弦长公式,运用基本不等式,考查运算求解能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com