
分析 由题意画出图形,由已知条件求出D到平面PAB的距离,把三棱锥P-MBD的体积转化为三棱锥D-PBM的体积求解.
解答 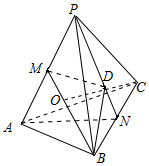 解:如图:
解:如图:
∵P-ABC为正四面体,且棱长为2,
∴C在底面PAB的射影为底面三角形PAB的外心O,也是重心,
则BM=$\sqrt{3}$,BO=$\frac{2\sqrt{3}}{3}$,
∴$CO=\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$,
又N为BC的中点,PD=2DN,
D到面PAB的距离为$\frac{2}{3}×\frac{1}{2}CO=\frac{1}{3}×\frac{2\sqrt{6}}{3}=\frac{2\sqrt{6}}{9}$,
而${S}_{△PBM}=\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$,
∴${V}_{P-MBD}={V}_{D-PBM}=\frac{1}{3}×\frac{\sqrt{3}}{2}×\frac{2\sqrt{6}}{9}=\frac{\sqrt{2}}{9}$.
故答案为:$\frac{\sqrt{2}}{9}$.
点评 本题考查棱柱、棱锥及棱台的体积,考查学生的空间想象能力和思维能力,训练了等积法在求多面体体积中的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{6}})$ | B. | $({0,\frac{1}{6}})∪({\frac{5}{6},\frac{5}{2}})$ | C. | $({0,\frac{1}{4}})∪({\frac{5}{4},\frac{5}{2}})$ | D. | $({0,\frac{1}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com