
已知 ,
,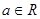
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点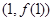 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在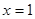 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(Ⅲ)是否存在实数 ,使
,使 在区间
在区间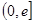 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅰ) (Ⅱ)
(Ⅱ)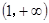 (Ⅲ)
(Ⅲ)
解析试题分析:(Ⅰ)求曲线在一点处的切线方程,一要抓切点(1,2),一要抓导数的几何意义即切线的斜率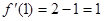 ,便求出切线方程
,便求出切线方程 ;(Ⅱ)先利用极值求出系数
;(Ⅱ)先利用极值求出系数 ,再利用
,再利用 及定义域
及定义域 ,求出单调递增区间为
,求出单调递增区间为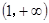 ;(Ⅲ)利用导数求某区间上的最值,要综合应用极值、单调性进行判定求解,特别对
;(Ⅲ)利用导数求某区间上的最值,要综合应用极值、单调性进行判定求解,特别对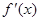 的形式、
的形式、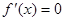 的根进行分类讨论.多见于单调函数、单峰(谷)函数.
的根进行分类讨论.多见于单调函数、单峰(谷)函数.
试题解析:(Ⅰ)函数 的定义域为
的定义域为 , 因为
, 因为 ,所以
,所以
当 时,
时,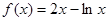 ,
, ,所以
,所以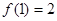 ,
,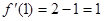
所以曲线 在点
在点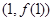 处的切线方程为
处的切线方程为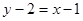 ,即
,即 . 3分
. 3分
(Ⅱ)因为 在
在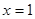 处有极值,所以
处有极值,所以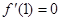 , 由(Ⅰ)知
, 由(Ⅰ)知 ,所以
,所以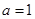
经检验,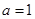 时
时 在
在 处有极值. 4分
处有极值. 4分
所以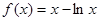 ,令
,令 ,解得
,解得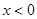 或
或 ;
;
因为 的定义域为
的定义域为 ,所以
,所以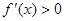 的解集为
的解集为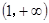 ,
,
即 的单调递增区间为
的单调递增区间为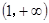 . 6分
. 6分
(Ⅲ)假设存在实数 ,使
,使 在区间
在区间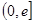 上有最小值3,由
上有最小值3,由 ,
,
① 当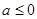 时,
时, ,
, 在
在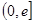 上单调递减,
上单调递减,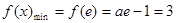 ,解得
,解得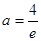 ,舍去. 8分
,舍去. 8分
②当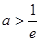 即
即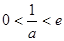 时,
时, 在
在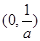 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,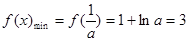 ,解得
,解得 ,满足条件. 10分
,满足条件. 10分
③ 当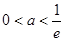 即
即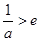 时,
时, ,
,
所以 在
在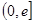 上单调递减,
上单调递减,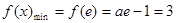 ,解得
,解得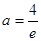 ,舍去.
,舍去.
综上,存在实数 ,使
,使 在区间
在区间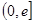 上的最小值是3. 12分
上的最小值是3. 12分
考点:导数的几何意义 导数的应用 分类讨论思想


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com