练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi(单位：千元)与月储蓄yi(单位：千元)的数据资料，算得＝80，＝20，＝184，＝720.

    (1)求家庭的月储蓄y对月收入x的线性回归方程y＝bx＋a；

    (2)判断变量x与y之间是正相关还是负相关；

    (3)若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．

    附：线性回归方程y＝bx＋a中，b＝，a＝－b ，其中，为样本平均值，线性回归方程也可写为


    解析：(1)由题意知n＝10，＝＝＝8，

    ＝＝＝2，

    又lxx＝－n2＝720－10×82＝80，

    lxy＝－n ＝184－10×8×2＝24，

    由此得b＝＝＝0.3，

    a＝－b＝2－0.3×8＝－0.4，

    故所求回归方程为y＝0.3x－0.4.

    (2)由于变量y的值随x值的增加而增加(b＝0.3>0)，故x与y之间是正相关．

    (3)将x＝7代入回归方程可以预测该家庭的月储蓄为y＝0.3×7－0.4＝1.7(千元)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    读下面程序，当输出的y的范围大于1时，则输入的x值的取值范围是(　　)

    A．(－∞，－1)                B．(1，＋∞)

    C．(－∞，－1)∪(1，＋∞)      D．(－∞，0)∪(0，＋∞)

    INPUT　x

    IF　x＞0　THEN

    　y＝SQRx

    ELSE

    　　y＝0.5^x－1

    END IF

    PRINT　y

    END
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工________人．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在育民中学举行的电脑知识竞赛中，将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组，绘制如图所示的频率分布直方图．已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05，第二小组的频数是40.

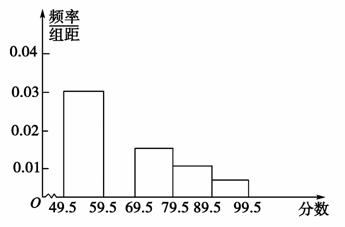
    (1)求第二小组的频率，并补全这个频率分布直方图．

    (2)这两个班参赛的学生人数是多少？

    (3)这两个班参赛学生的成绩的中位数应落在第几小组内？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    工人工资y(单位：元)与劳动生产率x(单位：千元)的回归方程为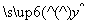＝50＋80x，下列判断正确的是(　　)

    A．劳动生产率为1 000元时，可估测工资为130元

    B．劳动生产率提高1 000元时，可估测工资提高80元

    C．劳动生产率提高1 000元时，可估测工资提高130元

    D．当月工资为250元时，劳动生产率为2 000元

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如上图所示，该程序框图所输出的结果是(　　)

    A．32         B．62        C．63       D．64

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    执行如图的程序框图，若p＝4，则输出的S＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f1(x)＝sin x＋cos x，记f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，

    fn(x)＝fn－1′(x)(n∈N*，n≥2)，则=            。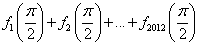

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，若函数恰有两个不同的零点，则实数的取值范围为       ．

    查看答案和解析>>

    同步练习册答案