
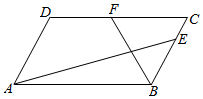
 ��ƽ���ı���ABCD�У�AB=4��AD=3����DAB=$\frac{��}{3}$����E��F�ֱ���BC��DC���ϣ���$\overrightarrow{BE}$=$2\overrightarrow{EC}$��$\overrightarrow{DF}$=$\overrightarrow{FC}$����$\overrightarrow{AE}$$•\overrightarrow{BF}$=��������
��ƽ���ı���ABCD�У�AB=4��AD=3����DAB=$\frac{��}{3}$����E��F�ֱ���BC��DC���ϣ���$\overrightarrow{BE}$=$2\overrightarrow{EC}$��$\overrightarrow{DF}$=$\overrightarrow{FC}$����$\overrightarrow{AE}$$•\overrightarrow{BF}$=��������| A�� | $-\frac{8}{3}$ | B�� | -1 | C�� | 2 | D�� | $\frac{10}{3}$ |
���� ��������ɵõ�$\overrightarrow{BE}=\frac{2}{3}\overrightarrow{AD}��\overrightarrow{CF}=-\frac{1}{2}\overrightarrow{AB}$�����������ӷ��ļ��������ɵõ�$\overrightarrow{AE}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}��\overrightarrow{BF}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$����������AB=4��AD=3����DAB=$\frac{��}{3}$���������������������$\overrightarrow{AE}•\overrightarrow{BF}$��ֵ��
��� �⣺$\overrightarrow{BE}=2\overrightarrow{EC}$��$\overrightarrow{DF}=\overrightarrow{FC}$��
��$\overrightarrow{BE}=\frac{2}{3}\overrightarrow{BC}=\frac{2}{3}\overrightarrow{AD}$��$\overrightarrow{CF}=\frac{1}{2}\overrightarrow{CD}=-\frac{1}{2}\overrightarrow{AB}$��
��$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$��$\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{CF}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$��
��$\overrightarrow{AE}•\overrightarrow{BF}=��\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}��•��\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}��$
=$\frac{2}{3}\overrightarrow{AB}•\overrightarrow{AD}-\frac{1}{2}{\overrightarrow{AB}}^{2}+\frac{2}{3}{\overrightarrow{AD}}^{2}$
=$\frac{2}{3}•4•3•cos\frac{��}{3}-8+6$
=2��
��ѡ��C��
���� �����������˺ͼӷ��ļ������壬��������ĸ���Լ����������������㼰����㹫ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{5}{2}$ | C�� | $\frac{7}{2}$ | D�� | $\frac{11}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʱ�� | ��14��10�� | ��14��11�� | ��14��12�� | ��15��1�� | ��15��2�� | ��15��3�� |
| ���������� | 7�� | ��11 | ��13 | ��12 | ��10 | ��8 |
| �����ؽ�ͨ�¹ʰ����� | ��14 | ��25 | ��29 | ��26 | ��22 | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{3}$��3�� | B�� | ��$\frac{1}{3}$��$\frac{4}{3}$�� | C�� | ��3��12�� | D�� | ��$\frac{4}{3}$��12�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com