
| 时间 | 14年10月 | 14年11月 | 14年12月 | 15年1月 | 15年2月 | 15年3月 |
| 雾霾天数 | 7 | 11 | 13 | 12 | 10 | 8 |
| 严重交通事故案例数 | 14 | 25 | 29 | 26 | 22 | 16 |
分析 (1)代入古典概型的概率公式计算;
(2)根据回归系数公式计算回归系数,得出回归方程;
(3)利用回归方程进行估计,检验.
解答 解:(1)剔除的2组数据不是相邻2个月的数据概率为P=1-$\frac{5}{{C}_{6}^{2}}$=$\frac{2}{3}$.
(2)$\overline{x}=\frac{11+13+12+8}{4}=11$,$\overline{y}=\frac{25+29+26+16}{4}=24$.
∴$\stackrel{∧}{b}$=$\frac{(11×25+13×29+12×26+8×16)-4×11×24}{1{1}^{2}+1{3}^{2}+1{2}^{2}+{8}^{2}-4×1{1}^{2}}$=$\frac{18}{7}$,$\stackrel{∧}{a}$=$24-\frac{18}{7}×11$=-$\frac{30}{7}$.
∴x的线性回归方程$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$.
(3)①当x=7时,$\widehat{y}$=$\frac{96}{7}$,当x=10时,$\widehat{y}$=$\frac{150}{7}$.
②当x=7时,|$\frac{96}{7}-14$|=$\frac{2}{7}$<2;
当x=10时,|$\frac{150}{7}-22$|=$\frac{4}{7}<2$.
∴线性回归方程是合情的.
点评 本题考查了线性回归方程的求解,古典概型的概率计算,属于基础题.


科目:高中数学 来源: 题型:解答题
 正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.
正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
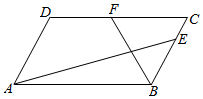 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )| A. | $-\frac{8}{3}$ | B. | -1 | C. | 2 | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com