
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 α为锐角,可得tanα>0,则“log2tanα>1”可得:tanα>2,$\frac{π}{4}<α<\frac{π}{2}$,可得:$2α∈(\frac{π}{2},π)$⇒“0<sin2α<$\frac{4}{5}$”,反之不成立,例如取α=$\frac{π}{12}$.即可判断出结论.
解答 解:∵α为锐角,∴tanα>0,
则“log2tanα>1”⇒tanα>2,⇒$\frac{π}{4}<α<\frac{π}{2}$,
∴$2α∈(\frac{π}{2},π)$⇒“0<sin2α<$\frac{4}{5}$”,反之不成立,例如取α=$\frac{π}{12}$.
∴“log2tanα>1”是“0<sin2α<$\frac{4}{5}$”的充分不必要条件.
故选:A.
点评 本题考查了不等式的性质、简易逻辑的判定方法、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
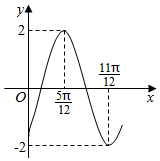
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 14年10月 | 14年11月 | 14年12月 | 15年1月 | 15年2月 | 15年3月 |
| 雾霾天数 | 7 | 11 | 13 | 12 | 10 | 8 |
| 严重交通事故案例数 | 14 | 25 | 29 | 26 | 22 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 56 | B. | 7 | C. | -56 | D. | -7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com